Accueil

Solutions 1 à 20

1. Roses de Pascale

Pour souligner la fête des Mères, Pascale a décidé d’organiser une fête dans sa municipalité. Pour cela, elle a acheté des roses. Dans un premier temps, elle donne le quart de ses roses sauf 3. Dans un second temps, elle donne le tiers de ce qui reste sauf 2. Il lui reste alors 100 roses pour une autre distribution.

Combien Pascale a-t-elle acheté de roses ?

2. Bâtons de hockey

Un organisme sportif distribue 100 bâtons de hockey à 36 joueurs. Chaque joueur de 12 ans en reçoit 4. Chacun de 11 ans en reçoit 3 et chacun de 10 ans en reçoit 2. L’organisme veut que le plus grand nombre possible de joueurs de 12 ans reçoivent des bâtons.

Combien y a-t-il de joueurs de chaque âge qui reçoivent des bâtons de hockey ?

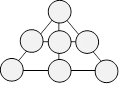
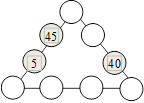
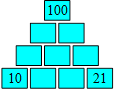
3. Sacs de noisettes

Mathias fait six sacs de noisettes qui contiennent respectivement 30, 31, 32, 33, 35 et 37 noisettes. Il veut placer les sacs dans les cellules de la figure ci-après. Il doit y avoir 100 noisettes dans chaque rangée de trois cellules reliées par une droite.

En tout, combien doit-on trouver de noisettes dans les trois cellules rouges ?

4. Pensées de l’An

C’est le jour de l’An. Tante Lorraine a invité ses jeunes neveux et nièces à la fête. Tous ont répondu à l’invitation, sauf 3 qui sont à l’extérieur du pays. Chaque jeune présent a préparé une carte de pensées pour chacun des autres aussi présents. En arrivant, chacun doit déposer le tout dans une corbeille. Tante Lorraine a compté entre 100 et 125 cartes.

Combien Tante Lorraine a-t-elle de neveux et de nièces ?

5. Pains bienvenus

Un club social distribue 100 pains à 100 personnes. Une femme adulte reçoit deux pains, une jeune femme un demi pain, et une adolescente un quart de pain. Parmi les 100 personnes présentes, il y a plus d’adolescentes que de toutes autres.

Combien y a-t-il de femmes adultes, de jeunes femmes et d’adolescentes ?

6. Rêve de papillotes

Le jeune Antoine fit un rêve. Il transportait un sac de 100 papillotes. Devant son école, il y avait des petits lutins. Au premier, il donna moins du quart de ses papillotes. Par la suite, il en donna 3 de plus d’un lutin à l’autre. À la fin, il resta une papillote dans son sac.

Combien y avait-il de petits lutins ?

7. Croix de Charlyne

Charlyne veut placer dans les cases de la croix ci-après 9 entiers différents dont la somme dans chaque rangée est 100.

Quel est le plus grand nombre qui peut être placé au centre ?

8. Coins de Cédric

Cédric veut remplir une grille d’ordre 3 dans laquelle on doit trouver 9 entiers consécutifs. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être la même. De plus, la somme des nombres des quatre coins doit être 100. Deux nombres sont en bonne position.

Complétez la grille.

9. Cerises de Sophie

Dix enfants sont en ligne. Dans un premier temps, Sophie distribue 100 cerises en parts égales. Dans un second temps, les autres cerises sont distribuées de telle manière que chaque enfant a une cerise de plus que son voisin. Si on soustrait le nombre de cerises que Sophie avait au départ et le nombre donné à l’enfant qui en a eu le plus, on obtient 171.

Combien Sophie avait-elle de cerises au départ ?

10. Kiosques d’Ophélie

Ophélie s’adonne au jeu des quatre kiosques avec une boîte de médaillons. Elle part du premier kiosque et visite chacun d’eux dans l’ordre. À chaque kiosque, elle reçoit ou donne des médaillons selon ce qui est écrit sur la façade. À la fin, Ophélie a 100 médaillons.

Combien Ophélie avait-elle de médaillons au début ?

11. Tours de piste

Une piste circulaire mesure 100 mètres. Lucie et Martin partent d’un même point. Lucie parcourt successivement la moitié, le tiers et le quart de cette longueur. Martin parcourt dans le sens contraire la moitié, le quart et le sixième de cette longueur.

À la fin du parcours, qui des deux est le plus proche du point de départ ?

12. Collections d’éléphants

Trois amis possèdent 100 éléphants. Adam dit : « Si je multiplie ma quantité d’éléphants par celle de Carl, j’obtiens 533. » Benoît ajoute : « Si je multiplie ma quantité par celle de Carl, j’obtiens 598. »

Combien chacun a-t-il d’éléphants ?

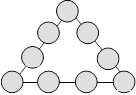
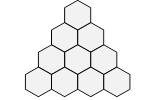
13. N de Nathan

Nathan a dessiné un N agrémenté de 7 cellules hexagonales. Il veut disposer 30, 31, 32, 33, 34, 35, 36 de façon que la somme soit 100 dans chacune des trois rangées de trois cellules reliées par une droite.

Quelle sera la somme des nombres des cellules marquées A et B ?

14. Carré d’Alexandre

Alexandre a composé un carré magique. La somme des nombres de chaque rangée horizontale, verticale et diagonale est 100. Deux nombres sont donnés.

Complétez le carré magique.

15. Distribution de médailles

Lors de la dernière compétition de jeux de stratégie, l’école Dubreuil a remporté 11 médailles, les unes en chocolat, les autres en caramel. Sur le marché noir, une médaille en chocolat vaut 10 pistoles et une médaille en caramel, 8 pistoles. La vente des médailles gagnées rapporterait alors 100 pistoles.

Combien l’école a-t-elle remporté de médailles de chaque sorte ?

16. Pommiers bienveillants

Pour souligner le temps des pommes, Marcelle a participé à un concours. À la première partie, elle a perdu 12 pommes. Elle a alors emprunté à un pommier autant de pommes qu’il en restait dans son panier. La même situation s’est produite aux trois parties suivantes. Après la quatrième partie, Marcelle avait 100 pommes.

Combien Marcelle avait-elle de pommes au début ?

17. Cartes d’Alicia

Sur un côté d’une carte postale, Alicia trace des droites parallèles et trois droites obliques parallèles de moins que des droites déjà tracées. Ayant compté le nombre de points d’intersection, elle déclare que c’est un nombre supérieur à 100, mais le plus près possible de 100.

Combien la carte contient-elle de lignes parallèles ?

18. Châteaux de François

François dessine deux châteaux en une première rangée horizontale. Par la suite, il augmente d’un château à chaque rangée. Il dessine ainsi 100 châteaux. Voici la situation pour les quatre premières rangées :

Déterminez la position du 100^e château.

19. Romans de Mégane

Mégane vient de finir de lire son 100^e roman. Elle le classe dans sa bibliothèque qui comprend quatre tablettes.

• Il y a 47 livres dans les deux tablettes du haut.

• Il y a 48 livres dans les deux tablettes du milieu.

• Il y a 4 livres de plus sur la tablette du bas que sur celle du haut.

Combien y-a-t-il de livres dans chacune des quatre tablettes ?

20. Cible de Jade

Sur du carton, Jade a préparé une cible. Avec un dard, quand elle atteint le centre, elle gagne 7 points ; quand elle atteint la couronne, elle gagne 5 points ; quand elle atteint l’extérieur de la cible, elle perd 3 points. Après 28 lancers, elle a réussi un lancer de plus dans le centre qu’à l’extérieur. Son score est alors de 100 points.

Combien de fois Jade a-t-elle atteint le centre de la cible ?

Solutions 21 à 40

21. Catherine voyage

Catherine part en randonnée en automobile pour quatre jours. Le premier jour, elle parcourt le tiers du trajet plus 5 kilomètres. Le deuxième jour, elle parcourt le tiers du trajet qui lui reste plus 6 kilomètres. Le troisième jour, elle parcourt le tiers du trajet qui lui reste plus 4 kilomètres. Le quatrième jour, elle parcourt les 100 kilomètres restants.

Combien de kilomètres la randonnée a-t-elle duré ?

22. Boules de Paul

Paul prend 100 boules numérotées. Il place d’abord 10 boules en deux rangées comme ci-après. Il complète les deux rangées vers la droite en plaçant les autres boules, tout en observant la même régularité dans chaque rangée et en ayant le même nombre de boules par rangée.

Quelle est la différence entre les deux derniers numéros de chaque rangée ?

23. Enfants comblés

Eusèbe répartit son avoir entre ses quatre enfants.

À Liane, il donne 100 florins, plus un quart de ce qui reste.

À Clara, il donne 100 florins, plus la moitié du montant donné à Liane.

À Mathieu, il donne 100 florins, plus un tiers du montant donné à Liane.

À Isaac, il donne 100 florins, plus un sixième du montant donné à Liane.

 Quel était l’avoir d’Eusèbe ?

24. Grille de Lucas

Lucas a rempli la grille ci-après avec des binômes. Les lettres A, B et C représentent chacune un nombre. La somme des nombres de chaque rangée horizontale et verticale doit être 100.

Remplissez la grille avec des nombres.

25. Somme de Dorothée

Dorothée recherche quatre nombres de deux chiffres dont la somme est 100. Son ami lui dit : « Un de ces nombres est 16 et les trois autres sont formés de chiffres de 1 à 6 chacun une seule fois. Les trois nombres manquants sont en ordre croissant. »

Combien y a-t-il de possibilités d’avoir une somme de 100 ?

26. Zigzag de Charlotte

Charlotte a écrit les nombres consécutifs à partir de 2 dans la grille ci-après selon une certaine régularité.

Quelle est la position de la case dans laquelle on peut écrire 100 ?

27. Coccinelle de Sandrine

Dans son grenier, Sandrine trouve un minuscule podomètre qui marque les mètres entiers. Elle l’attache au cou de sa coccinelle. Celle-ci doit rendre visite à ses amis.

• La première heure, la coccinelle parcourt le huitième de la distance totale plus 5 mètres.

• La deuxième heure, elle parcourt le quart de la distance qui reste plus 6 mètres.

• La troisième heure, elle parcourt la moitié de la distance qui reste plus 8 mètres.

Il lui reste encore 100 mètres à parcourir avant de se rendre à destination.

Quelle est la distance totale parcourue par la coccinelle pendant les trois premières heures ?

28. Épluchettes de noisettes

Les membres de la famille Arbrisseau cueillent chaque automne plusieurs poches de noisettes. Ils organisent des épluchettes et se font chacun des provisions. À partir du 12 octobre cette année-là, Laurie mange 3 noisettes par jour ; Mathis mange 7 noisettes le deuxième jour sur 2 ; Florence mange 10 noisettes le troisième jour sur 3.

À quelle date auront-ils mangé au moins 100 noisettes en tout ?

29. Cœurs d’Xavier

Xavier a dessiné quatre figures avec des cœurs et des cercles. Puis, il continue selon la même régularité jusqu’à ce que la dernière figure ait 100 cercles à la base du triangle intérieur.

Combien cette figure devra-t-elle contenir de cœurs ?

30. Cahier de Brigitte

Dans son grand cahier, Brigitte s’est amusée à écrire à la suite les chiffres de 1 à 9 comme suit : 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 … Chaque ligne est formée de 100 chiffres. Chaque page contient 100 lignes.

Quel serait le chiffre écrit à la fin de la première page du cahier ?

31. Triangle d’Yvonne

Yvonne dispose les entiers consécutifs en un triangle comme ci-après. Puis, elle continue à écrire les nombres selon la même régularité.

Quelle sera la moyenne des nombres de la ligne où se trouve 100 ?

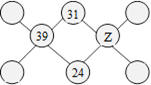
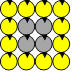
32. Cellules de Zacharie

Dans la figure ci-après qui contient huit cellules, Zacharie a placé 31, 39 et 24. Il désire compléter la figure pour que la somme des nombres de chaque rangée de trois cellules reliées par une droite soit 100. De plus, la somme des quatre coins doit être 154.

Quel nombre devra apparaître dans la cellule marquée Z ?

33. Banane de Simone

Simone a écrit l’égalité ci-après. Chaque lettre représente un chiffre différent. Aucune lettre n’a la valeur 0 ou 1.

B A + N A + N E = 100

Quelles sont les valeurs possibles de N ?

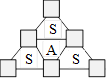
34. Triangle de Sara

Sara a formé la figure ci-après. Elle veut écrire des nombres dans les cases. Pour chacun des trois petits triangles marqués d’un S, la somme des trois cases des sommets est 100. De plus, la somme des trois sommets du grand triangle est 98.

Quelle sera la somme des sommets du petit triangle marqué A ?

35. Couples de Jules

Jules décompose chaque nombre en la somme de deux entiers différents. Par exemple, pour 32, Jules écrit 12 + 20, 13 + 19, 14 + 18, etc. Le premier nombre du couple est toujours plus petit que l’autre.

En combien de couples peut-on décomposer 100 comme la somme de deux entiers différents dont l’un est un multiple de 3 ?

36. Pause d’avelines

Hélice travaille cinq jours par semaine, sauf le mercredi et le vendredi. Quand elle est en congé, elle mange cinq avelines par jour et n’en reçoit pas. Quand elle travaille, elle en reçoit trois par jour et n’en mange pas, sauf le dimanche où elle n’en reçoit pas et en mange deux. Hélice a commencé à travailler le mardi 1^er février d’une année bissextile. Son sac contenait alors 100 avelines.

Combien aura-t-elle d’avelines le 1^er mars au soir ?

37. Haut de Victor

Victor a dessiné la figure ci-après. Dans les cercles, il veut placer des nombres, pas nécessairement des entiers, pour que la somme des cercles reliés par une droite soit 100.

Quel est le nombre qui doit être placé dans le cercle supérieur ?

38. Pamplemousses d’Éloïse

Éloïse distribue 100 pamplemousses dans trois boîtes. À son patron, qui veut connaître le nombre de fruits par boîte, elle dit : « J’élève au carré le nombre de fruits de chacune des boîtes. Dans ce cas, la somme des carrés des deux premières boîtes est 2669 et celle des carrés des deux dernières boîtes est 1954. »

Combien y a-t-il de pamplemousses par boîte ?

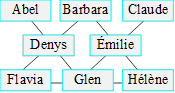
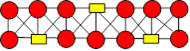
39. Confort pour l’hiver

Huit amis ont acheté des articles divers en vue d’affronter le prochain hiver.

? Claude et Émilie ont dépensé 65 roubles à eux deux.

? Les huit ont dépensé respectivement 15, 20, 25, 30, 35, 40, 45 et 50 roubles.

? Le nombre total de roubles dans chaque rangée de la figure suivante est 100.

Combien Barbara a-t-elle dépensé ?

40. Melons de Gervaise

Il est 21 heures. Depuis le matin, Gervaise a vendu plus de melons que d’habitude. Son amie qui travaille dans un kiosque voisin est anxieuse de connaître la quantité de melons vendus. Alors, Gervaise lui dit : « J’ai choisi un nombre. J’ai additionné 6 à ce nombre. J’ai multiplié le résultat par 6. J’ai soustrait 6. J’ai divisé par 6. J’ai obtenu 100 comme résultat. Le nombre que j’ai choisi c’est le résultat de mes ventes ».

Combien Gervaise a-t-elle vendu de melons depuis le matin ?

Solutions 41 à 60

41. Rangées de Gabrielle

Gabrielle a écrit trois nombres dans une grille carrée. Elle voudrait introduire d’autres nombres pour que la somme soit la même dans chaque rangée horizontale, verticale et diagonale.

Complétez le carré.

42. Suite d’Isaac

Isaac écrit les nombres suivants : 21, 23, 26, 30, 35, 41, 48, 56, 65, … D’un nombre à l’autre, l’augmentation est de 2, 3, 4, 5, 6, … qui se poursuit selon la même régularité.

Quel est le 100^e chiffre qu’Isaac écrira ?

43. Pruneaux de Roméo

Roméo désire remplir un sac qui contient déjà 2 pruneaux. Pour ce faire, dans une première opération, il y place 5 pruneaux. Dans une deuxième opération, il enlève 2 pruneaux. Puis il fait successivement les deux mêmes opérations.

Combien d’opérations Roméo aura-t-il effectuées quand il y aura 100 pruneaux dans le sac ?

44. Bâtonnets de Zoé

Zoé compose des grilles carrées avec des bâtonnets. Sur le contour, elle place des bâtonnets rouges et à l’intérieur des bleus. Elle désire connaître le nombre de bâtonnets nécessaires pour composer une grille carrée de 100 cases. Voici un exemple d’une grille 3 × 3 :

Déterminez le nombre de bâtonnets bleus qui seront nécessaires dans une grille carrée de 100 cases.

45. Marché de Nathaniel

Nathaniel se présente dans un marché du quartier. « Je veux, dit-il, 100 ananas, un certain nombre dans des sacs de trois ananas et le reste dans des sacs de quatre ananas. J’aimerais que le nombre de sacs de chaque groupe soit le plus rapproché possible ».

Combien de sacs de chaque groupe Nathaniel recevra-t-il ?

46. Partage de tartes

À la boulangerie Casse-croûte, on vient de terminer la cuisson de 100 tartes, les unes aux raisins et les autres aux bleuets. La patronne dit : « Si je livrais les tartes aux raisins en parts égales à 6 clients, il me resterait une tarte. Si je livrais les tartes aux bleuets en parts égales à 8 clients, il me resterait aussi une tarte. De plus, chaque client recevrait le même nombre de tartes ».

Combien y a-t-il de tartes pour chaque fruit ?

47. Fille délurée

Mélanie dit à ses compagnes :

• Multipliez l’âge que j’avais il y a 5 ans par l’âge que j’aurai dans 5 ans.

• Additionnez l’âge que j’avais il y a 5 ans et mon âge actuel.

• Soustrayez les deux résultats et vous obtiendrez 100.

Quel est l’âge actuel de Mélanie ?

48. Suites de Jérémie

Jérémie a préparé un tableau carré de 100 cases dans lequel des lettres et des nombres sont placés selon une certaine régularité. Les trois premières lignes du tableau sont données.

Que devra-t-on inscrire dans la 100^e et dernière case ?

49. Transfert de vin

Paul a deux tonneaux de vin qui contiennent ensemble 100 litres. Il verse un quart du premier tonneau dans le deuxième. Ensuite, il prend un quart du deuxième tonneau et verse le contenu dans le premier. Il retire 22 litres du premier tonneau pour l’usage de ses amis. Les deux tonneaux ont alors la même quantité.

Quelle était la quantité de vin dans chaque tonneau ?

50. Magie de Mia

Mia veut construire un carré magique d’ordre 3 en plaçant 8 au centre de la première ligne. La somme des autres entiers doit être 100. De plus, la somme des nombres doit être la même dans chaque ligne, colonne et diagonale.

Composez ce carré magique.

51. Pommes de Lucas

Lucas veut apporter 100 pommes à la maison en passant par une route surveillée. Il sait qu’à la première barrière, on lui réclamera le sixième de sa récolte. À la deuxième barrière, il devra donner un cinquième de ce qui lui reste. À la troisième barrière, il devra donner le quart de ce qui lui reste. Il veut aussi donner 20 pommes à son voisin avant d’entrer chez lui.

Combien Lucas devra-t-il acheter de pommes pour être certain d’en apporter 100 à la maison ?

52. Stylos de Guillaume

Guillaume a une boîte de stylos d’encre noire et une autre de stylos d’encre rouge. Il place 100 stylos en une rangée : un noir, un rouge, deux noirs, un rouge, trois noirs, un rouge et ainsi de suite. Il y a toujours un seul stylo rouge par intervalle et les noirs augmentent de façon consécutive.

Quelle sera la couleur de l’encre du 100^e stylo ?

53. Couleurs de Samuel

Dans une grille, Samuel dessine un cœur, passe une case et dessine un trèfle, passe trois cases et dessine un cœur. Il refait les mêmes opérations comme dans cette grille 5 × 5 :

Quelle devrait être la plus petite grille carrée qui permettra de disposer au moins 100 cœurs et 100 trèfles ?

54. Allumettes de Nathaniel

Nathaniel a construit une grille 2 × 2 avec des allumettes. Il a dû utiliser 12 allumettes. Une boîte d’allumettes en contient 100.

Combien de boîtes d’allumettes seraient nécessaires pour construire une grille 100 × 100 ?

55. Modèle de Claude

Claude a dessiné cette grille qui est formée de 18 cases. Il y compte 8 carrés 2 × 2.

Il prolonge la figure en accolant à droite 100 cases dans chaque rangée horizontale.

Combien pourra-t-on compter de carrés 2 × 2 dans cette nouvelle figure ?

56. Points de mérite

L’enseignante Marcelle a décidé de distribuer 100 points de mérite aux quatre élèves qui se sont absentés le moins souvent pendant l’année scolaire. Anne s’est absentée une demie journée, Jacob une journée, Karl une journée et demie, et Mélodie deux journées.

Combien chacun recevra-t-il de points de mérite proportionnellement à son dossier ?

57. Table de Léo

Léo produit une table d’addition pour les nombres de 1 à 100. Il écrit ces nombres dans l’ordre sur la première ligne et dans la première colonne. Par la suite, il additionne. Voici un exemple pour les nombres de 1 à 5 :

Quelle est la somme des nombres inscrits par Léo dans sa table pour les nombres de 1 à 100 ?

58. Grille de Benjamine

Benjamine a écrit 100 dans la grille carrée ci-après. Elle veut compléter la grille de façon que la somme soit 291 dans chaque rangée horizontale, verticale et diagonale. Les neuf éléments doivent être des nombres consécutifs. De plus, il y a une différence de 8 entre le terme central de la première ligne et celui de la dernière ligne.

Complétez la grille carrée.

59. Rêve de Clotaire

Cette nuit, Clotaire a rêvé que des coccinelles numérotées se promenaient sur les côtés d’un triangle. Les numéros sont les multiples de 5 à partir de 5 jusqu’à 45. À un moment donné, trois coccinelles étaient réparties comme ci-après. Les autres coccinelles doivent être placées pour que la somme des numéros soit 100 sur chaque côté du triangle.

Quel sera le numéro de la coccinelle placée dans le coin inférieur droit ?

60. Multiples de Julia

Dans une grille carrée de 100 cases, Julia fait la multiplication pour les nombres de 1 à 10. Voici un exemple avec une grille 5 × 5 pour les nombres de 1 à 5 :

Quelle est la somme des produits que Julia pourra inscrire dans sa grille pour les nombres de 1 à 10 ?

Solutions 61 à 80

61. Tableau de Violette

Dans les cases jaunes du tableau rectangulaire ci-après, Violette veut placer huit nombres dont la somme est 260. La somme dans chaque rangée diagonale de trois cases doit être 100. Dans deux coins opposés, les nombres 25 et 35 sont en bonne position.

Quelle sera la somme des nombres des deux autres coins opposés ?

62. Rectangle de Sébastien

Sébastien a décidé de construire un rectangle magique. Il a d’abord écrit 15 et 45. Il doit placer en plus deux 5, deux 20, deux 25, deux 30 et deux 40. La somme des nombres de chaque rangée horizontale doit être 100. Celle des nombres de chaque rangée verticale est unique, mais elle n’est pas donnée. Un nombre ne peut apparaître qu’une seule fois dans une rangée.

Quel sera le nombre qui devra apparaître dans le coin inférieur gauche ?

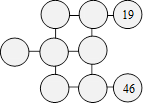
63. Cellules de Chloé

Chloé a dessiné la figure ci-après qui est composée de neuf cellules. Elle a placé les nombres 19 et 46 dans deux cellules. Elle veut disposer des nombres dans les autres cellules pour que la somme soit 100 dans chaque rangée de trois cellules reliées par une droite.

Quel est le nombre qui doit être placé au début de la deuxième rangée horizontale ?

64. Croix de Roxanne

Roxanne a reçu la tâche d’ériger sur la montagne une croix latine, soit une croix dont les branches sont d’égale longueur. Elle doit fixer 100 ampoules dans chaque rangée. Une représentation de la croix est donnée lorsqu’on a trois ampoules par rangée. Dans ce cas, elle aurait besoin de 24 ampoules.

De combien d’ampoules Roxanne aura-t-elle besoin si elle fixe 100 ampoules par rangée ?

65. Pruniers de Vivien

Vivien a planté 14 pruniers selon le schéma ci-après : deux arbres en première rangée, trois en deuxième rangée, quatre en troisième rangée. Il ajoute successivement un nouvel arbre pour chaque rangée inférieure.

Quel sera le rang du 100^e prunier dans la rangée où il sera planté ?

66. Décroissance de Robert

Robert écrit les nombres en ordre décroissant à partir de 100. Il insère alternativement un – et un + entre les nombres. Par exemple, il a écrit : 100 – 99 + 98 – 97 + 96 – 95 + 94. Chaque fois que Robert écrit un nombre, il fait le calcul approprié.

Quel sera le résultat quand Robert aura écrit 50 ?

67. Anniversaire de Tommy

Tommy a invité des amis à une collation. La table de famille peut s’allonger à volonté. Tommy prépare les trois premiers scénarios de disposition des invités. D’une table à l’autre, le nombre d’invités augmente de façon régulière.

Combien y aurait-il de personnes autour de la plus petite table où on pourrait placer le 100^e invité ?

68. Cellules d’Olive

Olive a dessiné la figure ci-après qui contient 10 cellules. Elle voudrait y placer 10 nombres qui font partie d’une suite dont la différence entre chaque terme est 4. La somme des nombres doit être 100 dans chaque rangée de deux ou de trois cellules reliées par une droite.

Est-ce possible de placer ces nombres dans la figure ?

69. Anne rougit

Anne a préparé la figure ci-après. Dans les cellules, elle veut placer les huit multiples différents de 5 à partir de 15 jusqu’à 50. La somme des nombres de chacune des quatre rangées de trois cellules reliées par une droite doit être 100. De plus, 15 et 45 doivent être placés dans les deux cellules du haut.

Quelle est la somme des nombres devant être placés dans les quatre cellules rouges ?

70. Façade de Jeannot

Jeannot a disposé des nombres sur les briques de cette façade. Tout nombre inscrit sur une brique, sauf ceux de la rangée du bas, est égal à la somme des nombres des deux briques inférieures qui touchent à celle-ci. Trois nombres sont donnés : 10, 21 et 100.

Quelle est la somme des quatre nombres de la rangée du bas ?

71. Triangle de Mathias

Mathias découpe neuf jetons marqués de nombres consécutifs. Le plus petit numéro est 100. Il veut placer les jetons sur la figure ci-après de façon que la somme de chaque rangée de quatre jetons soit la plus petite possible.

Quelle est cette somme ?

72. Carrés de Roberto
Roberto dessine une grille carrée de 100 cases. En suivant les lignes, il repère tous les carrés possibles à partir des carrés 1 × 1 jusqu’au carré 10 × 10.

Déterminez le nombre de carrés de toute grandeur.

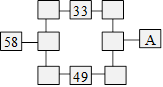
73. Figure d’Amélie

Amélie a inscrit 33, 58 et 49 dans la figure ci-après. Elle désire compléter la figure pour que la somme des nombres de chaque rangée de deux ou de trois cases reliées par une droite soit 100.

Quel nombre devra apparaître dans la case marquée A ?

74. Pairs de Julia

Dans une grille 3 × 3, Julia écrit le nombre 100 dans la position indiquée. Elle veut y placer des nombres pairs consécutifs pour que la somme soit la même dans chaque rangée horizontale, verticale et diagonale. Elle forme ainsi un carré magique.

Trouvez un carré magique dont la somme par rangée soit la plus petite possible.

75. À l’image de Fibonacci

Yolande forme une suite en écrivant d’abord deux fois le même nombre et en additionnant successivement les deux nombres précédents. Par exemple, elle choisit 3. La suite est :

3, 3, 6, 9, 15, 24, 39, 63, 102, ...

Quel nombre de départ Yolande devra-t-elle choisir pour avoir cinq fois 100, augmenté de 10, au 9^e rang ?

76. Ajouts de Christophe

Christophe a écrit trois nombres dans une grille carrée. Il voudrait introduire d’autres nombres pour que la somme soit la même dans chaque rangée horizontale, verticale et diagonale. La somme des autres nombres qui doivent apparaître dans la grille est 684.

Complétez la grille.

77. Guerre aux lapins

Du temps où les lièvres faisaient la guerre aux lapins, le grand Léporis entraînait les lièvres à se battre. Tous les matins, 100 lièvres en formation devaient se rendre à la Place Mimétique. Pour les inspecter, le chef disposait un groupe en un carré plein et un autre groupe en un carré à centre vide. Un bon matin, il y avait 28 lièvres de plus dans le carré vide que dans le plein.

Combien y avait-il de lièvres sur chaque côté du carré vide ce matin-là ? (Un carré plein est composé de n lièvres en n rangées. Un carré à centre vide comporte des lièvres seulement sur le contour, le nombre étant le même sur chaque côté.)

78. Noisettes d’Arnaud

Arnaud a ramassé des noisettes. Il prépare des sacs pour offrir à ses amis.

• Dans le premier sac, il met 10 noisettes.

• Dans le deuxième sac, il met 1 noisette de plus que dans le premier sac.

• Dans le troisième sac, il met 3 noisettes de plus que dans le deuxième sac.

• Dans le quatrième sac, il met 5 noisettes de plus que dans le troisième sac.

Arnaud continue à préparer d’autres sacs en ajoutant successivement 1, 3 et 5 noisettes de plus que dans le sac précédent. Il veut que le dernier sac contienne 100 noisettes.

Combien de sacs sont nécessaires ?

79. Tuiles de Michaël

Michaël prend des tuiles de 1 × 2 centimètres carrés. Il les place de façon à former le contour de trois carrés successifs. Il continue à former d’autres carrés selon la même régularité.

Déterminez le périmètre du carré intérieur lorsque la figure comprend 100 tuiles.

80. Bal des Finissants

Zénon et Gertrude sont le parrain et la marraine de Mario. En vue de son bal des Finissants, ceux-ci lui font les dons suivants :

• Oncle Zénon lui donne le quart de l’argent qu’il a sur lui.

• Tante Gertrude lui donne le même montant que Zénon.

• Oncle Zénon lui donne le tiers de l’argent qui lui reste.

• Tante Gertrude lui donne le même montant que Zénon.

Le filleul a alors 100 $.

Quel montant d’argent possédait l’oncle Zénon ?

 Solutions 81 à 100

81. Magie de Sara

Sara a composé un carré magique d’ordre 4. La somme des nombres est 100 dans chaque rangée horizontale, verticale et diagonale. Elle a effacé 9 nombres.

Rétablissez le carré magique.

82. Pique-nique annuel

Dans une école, 100 personnes participent à un pique-nique. Les garçons dépensent ensemble 225 euros. Chaque fille dépense un euro de plus qu’un garçon. Si on soustrait 55 au montant total dépensé et si on divise par 5, on obtient un résultat de 100 euros.

Combien y a-t-il de garçons et de filles au pique-nique ?

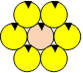
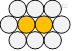
83. Oranges de Ludovic

Ludovic place d’abord une orange sur la table. Il entoure cette orange de telle manière que six oranges forment la première couronne comme il est illustré. On imagine que Ludovic colorie successivement une orange en rouge et deux en bleu dans chaque couronne.

Quelle serait la couleur de la 100^e orange ?

84. Arrosage d’arbres

Un fermier a planté 100 arbres en ligne droite sur sa terre. Chaque arbre est situé à un mètre l’un de l’autre. Il demande à son fils d’arroser chaque arbre. Une citerne est placée à trois mètres du premier arbre. Une chaudière d’eau permet d’arroser deux arbres. Un bon matin, chaudière en main, son fils entreprend l’arrosage. Il part de la citerne.

Quelle sera la distance parcourue par le fils pour arroser les 100 arbres tout en revenant à la citerne à la fin du travail ? On ne tient pas compte de la grosseur des arbres.

85. Points de Sara

Sara dessine 100 points en un carré. Avec sa règle, elle trace toutes les droites qui passent par trois points horizontalement, verticalement et obliquement. Voici un carré 4 × 4 :

Combien Sara pourra-t-elle tracer de telles droites dans un carré de 100 points ?

86. Losanges de Lucas

Lucas commence par dessiner une figure composée de trois losanges. Selon la même régularité, il trace vers la droite en alternance un losange muni d’un trait vertical et pas. Il se rend ainsi jusqu’à 100 losanges en tout. Quand il a terminé, il compte le nombre de traits droits qui apparaissent dans cette figure. Un trait peut être composé de deux segments comme dans deux losanges adjacents.

Combien de traits droits seraient nécessaires pour tracer la figure de 100 losanges ?

87. Tuiles de Mégane

Mégane prend six tuiles carrées et les assemble pour former une pièce rectangulaire 2 × 3. Elle pose ces tuiles sur une grille 100 × 100.

Trouvez le nombre maximal de pièces qui pourront être réparties sur la grille 100 × 100. Montrez de quelle façon on peut répartir les pièces.

88. Cure-dents de William

William est en train de construire la figure ci-après avec des cure-dents. Un cure-dents prend la place du côté d’un hexagone ou de deux côtés qui coïncident. Son père lui dit : « Dans cette figure, tu as quatre hexagones à la base. Serais-tu capable de compter le nombre de cure-dents si la base contenait 100 hexagones ? »

Quel serait le nombre de cure-dents nécessaire si la base contenait 100 hexagones ? 

89. Oranges de Zoé

Zoé place d’abord quatre oranges en un carré sur la table. Elle entoure ce carré de telle manière que 12 oranges forment la première couronne.

De combien d’oranges Laurie aurait-elle besoin pour composer la 100^e couronne ?

90. Cavalier de Lucas

Lucas prend un cavalier du jeu d’échecs et le place dans la case du coin supérieur droit d’une grille 100 × 100. Voici les premiers sauts d’un cavalier dans une grille 7 × 7 :

Combien de sauts au minimum le cavalier doit-il faire pour atteindre la case du coin inférieur droit dans une grille 100 × 100 ?

91. Croix de Bruno

Bruno trace une grille 100 × 100 dans laquelle il rogne un carré 2 × 2 dans chaque coin. Voici un exemple d’une grille 8 × 8 :

Combien peut-on compter de carrés 3 × 3 dans la croix d’une grille 100 × 100 ?

92. Fou de Carole

Carole prend un fou du jeu d’échecs et le place dans la case du coin supérieur gauche d’une grille 100 × 100. Normalement, un fou se déplace seulement en diagonale. Le fou de Carole parcourt 3 cases vers la droite et s’arrête. Il parcourt une case vers la gauche et s’arrête. Il continue selon la même régularité. Voici les premiers déplacements d’un fou dans une grille 9 × 9 :

Sur quelle case de la 100^e rangée horizontale le fou terminera-t-il sa course ?

93. Monnaie d’Antoine

Antoine a placé 10 pièces de monnaie : 2 au centre et 8 dans la première couronne. Il continue à placer des pièces pour former d’autres couronnes.

Combien devrait-il y avoir de pièces dans la 100^e couronne ?

94. Locomotive de Julia

Julia dessine la figure ci-après qui est composée de cercles, de rectangles et de droites. Selon la même régularité, elle prolonge cette figure vers la droite. Quand Julia a terminé, elle a tracé 100 perpendiculaires de façon verticale.

Combien peut-on compter de groupes de deux cercles voisins reliés par une droite lorsque la figure est composée de 100 perpendiculaires ?

95. Briques de Sophia

Sophia a disposé 10 briques comme ci-après. Elle a écrit 100 sur la brique du haut. Sauf pour la rangée inférieure, le nombre inscrit sur une brique est égal à la somme des nombres des deux briques inférieures qui touchent à celle-ci. Pour arriver à 100, Sophia a écrit une suite de quatre entiers consécutifs sur la rangée du bas.

Quelle est cette suite de quatre entiers consécutifs ?

96. Boules de Tristan

Tristan a récupéré 100 boules de tennis. Il prépare des figures de boules selon une certaine régularité. Les quatre premières figures sont données.

Quel sera le rang de la figure où sera placée la 100^e boule ? Quelle sera la position de cette boule dans la figure ?

97. Étoile capricieuse

Johanne numérote 10 jetons de 20 à 29. Elle veut placer les jetons sur les intersections de la figure ci-après. La somme des numéros de chaque rangée de quatre jetons doit être 100. Après plusieurs essais, elle n’a pas réussi. Son ami croit que c’est impossible.

L’ami a-t-il raison ? Si oui, pourquoi ?

98. Grille d’Annie

Annie désire placer les nombres de 8 à 32 dans une grille 5 × 5. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être 100. Annie a d’abord placé 12 nombres.

Complétez la grille.

99. Un centenaire

René a vu le jour le 18 avril 1999. C’était un dimanche. On suppose que René dépassera 100 ans.

Quel sera le jour de la semaine quand René fêtera ses 100 ans, soit le 18 avril 2099 ?

100. Tableau d’Océane

Océane a préparé le tableau suivant dans lequel les nombres de chaque ligne se suivent selon leur régularité propre. Elle prolonge le tableau vers la droite. Elle fait la somme des deux nombres de chaque colonne. Par exemple, la somme pour la sixième colonne est 38.

Trouvez la somme des nombres de la 100^e colonne.

FIN

Accueil