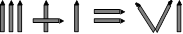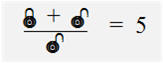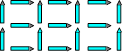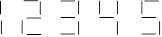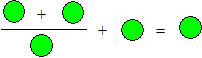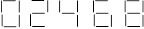|
(Dessin réalisé au primaire) Contactez-moi : cejean@charleries.net |
Les charleries Bienvenue sur mon blogue, Ce blogue contient des souvenirs, des anecdotes, des opinions, de la fiction, des bribes d’histoire, des récréations et des documents d’archives. Charles-É. Jean |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Petits problèmes plaisants Par Charles-É. Jean |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce recueil contient 150 problèmes courts qui font appel à des
connaissances mathématiques et logiques élémentaires. Les problèmes
s’adressent aux amateurs de 9 à 99 ans. Les stratégies de résolution qui
s’appliquent sont généralement à la portée des jeunes.
Amusez-vous bien ! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Solutions | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.
Châteaux recherchés
Les numéros civiques de cinq châteaux sont 1001, 1002, 1003, 1004 et
1005. La somme des numéros est 3009 dans chacune des deux rangées de
trois châteaux.
2.
Trinaires de Coralie
Coralie recherche les nombres dont la somme des chiffres est 3. On les
appelle nombres trinaires. Elle a trouvé les six plus petits nombres
trinaires : 3, 12, 21, 30, 102, 111.
Quel est le 12e nombre trinaire ?
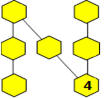
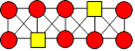
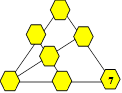
Alexis trace la figure ci-après qui comporte
une rangée de trois cases horizontalement et deux rangées de trois cases
en diagonale. Il découpe six jetons et les numérote de 1 à 6. Il place
le jeton 6 à l’endroit indiqué.
Placez les autres jetons dans les cases de façon que la somme des
numéros soit 10 dans chacune des trois rangées.
4.
Cartes de Théo
Théo a écrit une addition avec certains symboles du jeu de cartes.
Chaque symbole représente un chiffre différent. Deux symboles accolés
forment un nombre de deux chiffres.
§
ª
+
§
ª
©
§
Quelle est la plus grande valeur de
§ª
?
5. Jetons d’Isabelle
Isabelle prend cinq jetons carrés. Avec quatre jetons, elle forme un
carré et dispose l’autre jeton à droite de l’un déjà en place. Puis,
elle dessine la figure sur du papier.
Combien cette figure a-t-elle de côtés ?
6.
Feu d’Antoine
Avec des allumettes, Antoine a écrit en chiffres romains : 3 + 1 = 6. En
réalité, cette égalité est fausse.
Déplacez une allumette pour avoir une égalité vraie.
7. Dés de Mia
Mia prend deux dés : un bleu et un rouge.
Elle lance les deux dés en même temps.
À chaque coup, elle voudrait obtenir un total de 8 points.
De combien de façons différentes Mia peut-elle obtenir ce total ?
8.
Pont de William
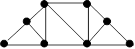
Ayant vu la structure du pont Jacques-Cartier pour la première fois,
William a été impressionné. Il dessine huit points et les relie par des
traits droits.
Combien de triangles de toute grandeur peut-on compter dans cette figure
?
9.
Carré de Jacques
Jacques dessine 16 points en un carré. Il veut savoir combien on peut
tracer de droites qui passent par trois points en ligne droite
horizontalement, verticalement et obliquement.
Combien de telles droites peut-on compter ?
10. Verger accueillant
Ben cueille 10 pommes dans le verger de son père. Il les numérote de 1 à
10. Il veut former des groupes de trois pommes dont la somme des numéros
est 15.
Combien peut-on former de groupes de trois pommes si, dans chaque groupe, les numéros sont différents ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11. À la cafétéria
Au menu d’une cafétéria, on retrouve un choix de trois mets principaux :
pâté chinois, spaghetti italien et lasagne. Il y a deux desserts :
salade aux fruits et yogourt. Gilles désire prendre une combinaison
différente à chaque repas.
Combien de repas seront nécessaires pour épuiser toutes les combinaisons
?
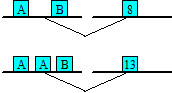
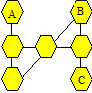
12. Balances en équilibre
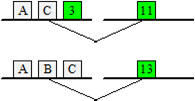
Des objets A, B et C sont déposés sur les plateaux de deux balances. On
y trouve aussi des poids de 3, 11 et 13 grammes qui servent à équilibrer
les plateaux. Chaque objet de même lettre a le même poids.
Combien l’objet B pèse-t-il ?
13. Couleurs au hockey
Josué prend 28 rondelles et les peint les unes en rouge et les autres en
bleu. Après le séchage, en une rangée, il place une rouge, une bleue,
une rouge, deux bleues, une rouge, trois bleues et ainsi de suite. Il y
a toujours une seule rondelle rouge par intervalle et les bleues
augmentent de façon consécutive.
Quelle sera la couleur de la dernière rondelle ?
14. Ouvert ou fermé
Jacob a composé une fraction avec des cadenas en deux positions. Chaque
forme de cadenas correspond à un nombre différent inférieur à 10, à
l’exception de 1.
Quelle est la valeur de
Ï
+Ð
?
15. Jetons de Guylaine
Guylaine découpe cinq jetons. Elle les numérote et les place dans cet
ordre.
Insérez des signes + et
´
entre les jetons de façon que le résultat soit 65.
16. Quatuors de Marius
Marius a trouvé un groupe de quatre nombres dont la somme est 24. Le
voici :
Combien de sommes sont possibles avec trois de ces quatre nombres ?
17. Neuvaine de Carole
Carole veut placer chacun des chiffres de 1 à 9 une seule fois dans
l’addition de façon que la somme soit vraie. Trois chiffres sont en
bonne position.
3 ■ ■
+
■
4
■
■
■
8
Distribuez les six autres chiffres.
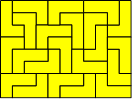
18. Livia et ses L
Livia a tracé un rectangle. Elle l’a partagé avec des L de même
grandeur. Chaque L est formé de quatre petits carrés.
Combien peut-on compter de L dans ce rectangle ?
19. Pommes de Rosalie
Rosalie numérote cinq pommes : 2, 5, 6, 8, 11. Elle veut les placer dans
des cases de la figure ci-après. La somme des numéros doit être la même
dans chacune des trois rangées de deux ou de trois cases.
Trouvez une façon de distribuer les cinq pommes.
20. Opérations de Florence
Florence dit à son ami : « 5 plus 7 font 12 et 12 fois 12 font 144. »
À l’aide d’opérations simples, agencez deux 5 et deux 7 de façon que le
résultat soit un peu moins de la moitié de 144, disons 70. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Solutions 21 à 40
Hugo admire son père. Il aime bien sa barbe bien taillée. En pensant à
cela, il écrit les lettres de BARBE. On peut lire le mot BARBE en
joignant les lettres voisines obliquement en tout sens.
Combien y a-t-il de façons de lire BARBE à partir du B du milieu de la
rangée supérieure ?
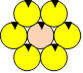
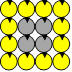
22. Oranges d’Alexis
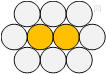
Alexis place d’abord une orange sur la table. Il entoure cette orange de
telle manière que six oranges forment la première couronne.
Combien Alexis pourra-t-il placer d’oranges dans la deuxième couronne ?
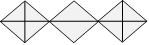
23. Erreurs d’Alexandre
En vue de se détendre avant une partie de dés, Alexandre dessine quatre
dés. Lorsque son ami voit ses dessins, il lui dit qu’il a fait une
erreur dans deux dés.
Quels sont les dés où il y a erreur ?
24. Lapins d’Arthur
C’est la semaine avant Pâques. Arthur a acheté des lapins en chocolat.
Il donne le tiers de ses lapins sauf 2. Il lui reste 16 lapins.
Combien de lapins Arthur a-t-il acheté ?
25. Macarons de Gertrude
Gertrude reçoit autant de macarons qu’elle en a. Elle donne alors cinq
macarons. À nouveau, elle reçoit autant de macarons qu’elle en a, puis
elle en donne cinq. Maintenant elle a 77 macarons.
Combien Gertrude avait-elle de macarons au début ?
26. Source de fierté
Alexia est fière de son prénom. Pour l’honorer, elle écrit l’addition
ci-après. Chaque lettre représente un chiffre différent. La valeur de L
est 5 et aucune lettre n’a une valeur supérieure à 6.
AL + EX = IA
Quelle est la valeur d’ALEXIA ?
27. Lettres de Mia
Mia aime les calculs avec les lettres. Son amie a écrit les deux
égalités suivantes.
A + B = 120
A – 36 = B
Quelles sont les valeurs de A et de B ?
28. Boutons de Georges
Georges a placé des boutons dans un coffret de neuf cases. Il y a le
même nombre de boutons dans chaque rangée horizontale, verticale et
diagonale. Le nombre de boutons dans les cases de la rangée du bas est
donné. Dans les autres cases, il y a 2, 4, 7, 8, 10 et 11 boutons.
Combien y a-t-il de boutons dans chacune des six autres cases ?
29. Panier de Caroline
Caroline arrive de la fruiterie avec un panier d’oranges. À l’aîné, elle
donne trois oranges. Au deuxième enfant, elle donne deux oranges de plus
qu’elle a donné à l’aîné. Au cadet, elle donne une orange de moins
qu’elle a donné au deuxième enfant. À la fin, il lui reste cinq oranges.
Combien d’oranges contenait le panier ?
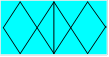
30. Losanges de Laurent
Pour la rentrée scolaire, Laurent s’est acheté une chemise tout en
losanges. Rendu chez lui, il trace cette figure.
Combien de traits droits ont été nécessaires pour tracer cette figure ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
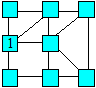
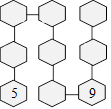
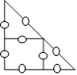
31. Jetons de Nathalie
Nathalie prépare sept jetons et les numérote de 1 à 7. Elle veut placer
les jetons dans les cellules pour que la somme soit 11 dans chacune des
trois rangées de trois cellules reliées par une droite. Le jeton 4 est
en bonne position.
Trouvez une façon de distribuer les autres jetons.
32. Une marche lente
Une tortue part du point de la troisième ligne de la grille. Elle visite
chacune des cases une et une seule fois en se déplaçant horizontalement
et verticalement. Elle termine sa marche à l’autre point.
Trouvez un chemin.
33. Début d’année scolaire
Myriam a acheté des cahiers et des crayons. Un cahier coûte cinq florins
et un crayon, trois florins de moins. Elle a acheté un crayon de plus
que de cahiers. En tout, elle a dépensé 23 florins.
Combien de cahiers Myriam a-t-elle achetés ?
34. Cure-dents de Mathis
Mathis a écrit les chiffres de 2 à 7 avec des cure-dents comme ceci.
Trouvez le plus petit nombre de trois chiffres différents qui utilisent
13 cure-dents.
35. Coloriage d’André
André dessine une grille carrée la plus petite possible. Il colorie
trois cases en bleu, cinq en rouge et deux en vert. Chacun de leur côté,
Sara et Bruno font de même dans cette grille. André reprend la grille et
colorie les cases qui restent en jaune.
Combien de cases seront coloriées en jaune ?
36. Mulot de Guillaume
Guillaume a donné un code à chaque lettre différente. Il a écrit trois
mots et mélange les codes de chacun.
M O N :
o
K
%
N U L :
u
Å
K
L O T :
o
Å
Y
Écrivez le code de MULOT.
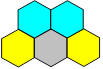
37. Géométrie de Rébecca
C’est le cours de géométrie. Pendant ce temps, Rébecca dessine la figure
suivante.
Combien peut-on y compter de groupes de deux cercles voisins reliés par
une droite ?
38. Déjeuner grillé
Ce matin, Francis a fait griller son pain un peu trop. Il s’assoit à son
bureau et trace une grille. Il y dessine cinq cœurs et cinq trèfles.
Combien y a-t-il
de carrés 3 × 3 qui contiennent exactement deux cœurs et deux trèfles ?
39. Tirelire de Sophie
Sophie prend les florins de sa tirelire. Elle en dépense le tiers pour
l’achat d’un vêtement. Puis, elle dépense cinq florins pour des
friandises. Il lui reste le tiers de ce qu’elle avait.
Combien de florins contenait la tirelire de Sophie ?
40. Parc de Raphaël
En revenant du parc où il a joué à la balle avec ses amis, Raphaël a
numéroté huit boules comme ceci.
Quel devrait être le numéro de la boule qui suit 34 dans la deuxième
rangée ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
41. Crayons d’Océane
Océane a disposé 17 crayons en un rectangle 2
´
3 comme ceci.
Combien faut-il ajouter de crayons pour construire un rectangle 3
´
4 ?
42. À mon drapeau
Dix drapeaux sont disposés en un cercle à un mètre l’un de l’autre. La
distance entre le dernier et le premier drapeau est de deux mètres.
Quelle est la distance la plus courte entre le 3e et le 9e
drapeau ?
43. Découpage de Mia
Mia a découpé huit petits carrés et les a disposés comme ceci.
Au minimum, combien de traits sont nécessaires pour partager la figure
en deux parties de même grandeur ?
44. Partage de cartes
Éva, Félix et Victoria ont ensemble 27 cartes de hockey. Éva donne trois
cartes à Félix. Félix donne deux cartes à Victoria. Ils ont alors le
même nombre de cartes.
Combien chacun avait-il de cartes avant le partage ?
45.
Lecture en tout sens
Rolande a écrit huit chiffres dans la grille ci-après. Elle dit à sa
jeune sœur : « Tu dois lire des nombres de trois chiffres
horizontalement et verticalement dans cette grille. Par exemple, tu
pourrais lire 375, 769 et 827 ».
Combien peut-on lire de nombres pairs de trois chiffres ?
46. Animal recherché
Nicole a écrit les lettres ci-après avec des bâtonnets
de même longueur.
Trouve le nom d’un animal qui exige 12 bâtonnets.
47. Grille d’Horace
Horace veut placer les nombres 5, 7, 8, 9, 10, 12 et 15 dans la grille
ci-après. La somme des nombres doit être 30 dans chaque ligne, colonne
et diagonale.
Complétez la grille.
48. Cartes d’Antoine
Avec des trèfles et des cœurs, Antoine a composé un rectangle 4
´
7. Il veut maintenant agrandir le rectangle vers la droite en continuant
à alterner le trèfle et le cœur autant horizontalement que
verticalement.
Combien de trèfles sont nécessaires pour composer un rectangle 6
´
10 ?
49. Repos de Fabien
En arrivant du travail, Fabien a écrit les cinq nombres ci-après. On
doit remplacer chaque nombre par la lettre qui correspond à son rang
dans l’ordre alphabétique.
1 3
5
8
22
En arrangeant les lettres autrement, trouvez le nom d’un animal.
50. Géométrie de Juliette
Juliette a écrit deux égalités en utilisant trois figures différentes.
Chaque figure est mise pour un chiffre. Deux figures accolées
correspondent à un nombre de deux chiffres.
♞
+
♥
=
▲
▲
+
▲
+
▲
=
♞♥
Quelle est la valeur de chacune des trois figures ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
51. Rues de Tommy
Tommy a écrit 20 lettres dans la grille ci-après. Il veut trouver des
carrés 2 × 2 qui contiennent les lettres de RUE au moins une fois.
Combien y a-t-il de tels carrés ?
52. Pommes de Madeleine
Madeleine répartit 10 pommes dans quatre plateaux disposés comme
ci-dessous. Chaque plateau doit avoir un nombre différent de pommes. De
plus, il doit y avoir le même nombre de pommes dans chaque rangée de
deux ou de trois plateaux.
Combien doit-il y avoir de pommes par rangée au maximum ?
53. Fruits de Coralie
Coralie arrive du marché avec un sac d’oranges. À sa fille qui veut
savoir combien le panier contient d’oranges, Coralie répond : « Si je
prends le nombre d’oranges et si j’additionne sa moitié, j’obtiens 42 ».
Combien Coralie a-t-elle d’oranges ?
54. Grille de Guillaume
Guillaume a préparé une grille 4 × 4. Il y a écrit chacun des chiffres
de 1 à 4 comme ci-après. Il faut placer des chiffres de 1 à 4 dans les
autres cases de façon que chaque chiffre apparaisse une seule fois dans
chaque ligne et dans chaque colonne. De plus, aucun 3 n’apparaît dans
les diagonales.
Complétez la grille avec des chiffres de 1 à 4.
55. Transfert de timbres
Alicia et Ludovic conversent.
Alicia : Si tu me donnais trois timbres, nous en aurions autant l’un que
l’autre.
Ludovic : Si tu me donnais deux timbres, j’en aurais trois fois plus que
toi.
Combien chacun a-t-il de timbres ?
56. Clous d’Xavier
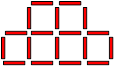
Xavier juxtapose six tuiles de même grandeur comme ci-dessous. Il pose
un clou à chaque sommet. Ainsi, il a besoin de 12 clous.
Par la suite, Xavier prend 12 tuiles et veut former un rectangle.
Combien Xavier aura-t-il besoin de clous au minimum ?
57. Magie d’Annabelle
Sur internet, Anabelle a trouvé un carré magique 4 × 4. Il est formé de
chacun des nombres de 1 à 16. La somme de chaque rangée horizontale,
verticale et diagonale est 34. Annabelle a effacé neuf nombres.
Reconstituez le carré magique.
58. Pistoles de Zacharie
Pour de menus articles, Zacharie dépense un certain nombre de pistoles un
lundi.
Par la suite, il dépense quatre pistoles de plus que le jour précédent.
Le vendredi, il a dépensé en tout 65 pistoles.
Combien de pistoles Zacharie a-t-il dépensé le mercredi ?
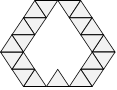
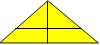
59. Triangles de Julienne
Julienne a tracé une figure avec des petits triangles. Par la suite,
elle a effacé les petits triangles de la partie intérieure.
Combien y avait-il de petits triangles dans cette partie ?
60. Grille de Michelle
Michelle doit écrire un chiffre dans chaque case de la grille ci-après.
On doit lire six nombres : trois en lignes et trois en colonnes.
Dans cette grille, écrivez les nombres 176, 397, 492, 526, 835 et 841. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
61. Réserve de jetons
Avec six jetons, Ariane a écrit l’addition ci-après dont la somme est
118. Il lui reste deux jetons numérotés 4.
Remplacez deux jetons par les deux 4 pour obtenir une somme de 133.
62. Cure-dents de Zacharie
Zacharie a écrit les chiffres de 1 à 5 avec des cure-dents comme ceci.
Trouvez deux nombres de deux chiffres dont la somme est 45 et qui
utilisent 20 cure-dents pour leur écriture.
63. Père et fille
Arthur dit à sa fille Réjeanne : « Il y a six ans, tu avais la moitié de
mon âge. Aujourd’hui, nos âges sont le renversé l’un de l’autre ».
Quel âge avait Arthur quand Réjeanne est née ?
64.
Carrés de Cédric
Cédric a tracé une grille rectangulaire qui est formée de 18 petits
carrés.
À part les petits carrés, combien peut-on compter de carrés de toute
grandeur dans cette grille ?
65. Astuce d’un père
« Si tu veux savoir l’âge de mon fils Raoul, de dire le père Losange,
trouve combien de fois on peut lire RAOUL dans ce triangle. La lecture
peut se faire dans tous les sens, même en zigzag, à la condition de
choisir une lettre voisine. Quand tu auras terminé, additionne 4 au
résultat ».
Quel est l’âge de Raoul ?
66. Addition de Léa
Léa veut faire une addition avec six chiffres en utilisant chacun des
ces chiffres : 2, 3, 4, 5, 7 et 8. Elle a trouvé l’égalité ci-après. Or,
73 n’est pas la plus grande somme.
Quelle est la plus grande somme ?
67. Pistoles d’Anatole
Anatole aime bien jouer en misant. Dans une première partie, il perd le
tiers de son argent. Dans une seconde partie, il gagne le quart de ce
qui lui reste. Il a alors trois pistoles de moins qu’au début.
Quel était l’avoir d’Anatole avant qu’il joue ?
68. Bocaux d’Ariane Ariane a numéroté cinq bocaux comme ceci.
Quels sont les trois bocaux dont la somme des numéros est 40 ?
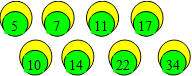
69. Tennis de Christophe
Christophe numérote neuf balles de tennis sur table comme ci-après.
Parmi elles, il y a un groupe de trois balles dont deux portent des
numéros consécutifs et dont la troisième a un numéro qui est la somme
des deux premières.
Choisissez ces trois balles.
70. Galaxie de Louise
Louise a
écrit ces deux égalités dans lesquelles chaque lettre représente un
nombre différent.
Quelle est la valeur de A et de B ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
71. Dominos de Mathieu
De son jeu de 28 dominos, Mathieu a pris les trois pièces suivantes. Il
veut les disposer en un rectangle pour que le total des points soit 6
dans la première colonne, 4 dans la deuxième et 2 dans la troisième.
Trouvez une façon de disposer les trois dominos.
72. Coloriage de Jasmine
Jasmine veut écrire le chiffre 2 dans ce rectangle en coloriant certains
petits carrés.
Combien de petits carrés doivent être coloriés ?
73. Automobiles en montre
Fiston Guillaume demande à son père combien il y a d’automobiles en
vente dans son garage. Son père lui répond : « Si je les compte trois
par trois, il en reste une. Si je les compte 4 par 4, il en reste une.
Il y en a moins de 20 ».
Combien le garagiste a-t-il d’automobiles à vendre ?
74. Loisirs de Gustave
Dans un moment de loisirs, Gustave a écrit l’addition ci-après dont la
somme est GUS. Chaque lettre représente un chiffre différent. Aucune
lettre ne peut être égale à 2.
U U + U U + U U + U U = G U S
Quelle est la valeur de GUS ?
75.
Pare-chocs accolés
Dans le stationnement d’un centre d’achats, Sophia a remarqué une file
de cinq automobiles placées pare-chocs contre pare-chocs. Les
automobiles sont dans le même sens et le pare-chocs de la première
automobile est contre le centre d’achats. Sophia dit à une amie :
« Comme magicienne, je peux prendre n’importe laquelle automobile dans
ma main et la retirer du groupe ».
Combien Sophia devrait-elle retirer d’automobiles au minimum pour que
chaque automobile puisse quitter ?
76. Morceaux de grille
Cynthia a préparé cette grille dans laquelle elle a écrit des nombres de
1 à 4.
Partagez cette grille en parties égales de façon que la somme soit la
même dans chaque partie.
77. Pesées de Maxime
Maxime dépose deux objets A et B sur deux balances à plateaux. Les poids
de 8 et de 13 grammes servent à équilibrer les plateaux.
Combien l’objet B pèse-t-il ?
78. Cellules de Catherine
Catherine veut construire cette figure avec des allumettes.
Combien d’allumettes seront nécessaires ?
79. Macarons de Victoria
Victoria a une collection de macarons. Elle en donne le tiers à sa sœur,
puis deux de moins à son frère. Il lui reste 10 macarons.
Combien Victoria avait-elle de macarons ?
80. Carré d’Arnaud
Quand Arnaud ne s’adonne pas à compter les carrés d’une grille, il écrit
les chiffres en caractères électroniques. Il a écrit 8 comme ci-après
avec sept segments. Il demande à son amie d’enlever un segment pour
avoir un carré.
Comment s’y prendra l’amie d’Arnaud ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
81. Choix de Sébastien
Sébastien a choisi un nombre de cinq chiffres différents.
• Le premier chiffre est dans 641 et non dans 182.
• Le deuxième chiffre est dans 452 et non dans 263.
• Le troisième chiffre est dans 804 et non dans 869.
• Le quatrième chiffre est dans 853 et non dans 782.
• Le cinquième chiffre est dans 346 et non dans 406.
Trouvez le nombre choisi par Sébastien.
82. Fraction de Jocelyn
Jocelyn découpe cinq jetons et les numérote 2, 3, 4, 5 et 8. Il prépare
la figure ci-après sur laquelle il veut placer les jetons sur les
cercles.
Trouvez une façon de disposer les jetons pour que l’égalité soit vraie.
83. Partage familial
Alicia partage un certain montant d’argent entre ses deux enfants.
Lucas reçoit un florin et le tiers du reste.
De ce qui reste, Chloé reçoit deux florins et le tiers du reste.
Après le partage, Alicia a un florin de plus que Lucas.
Combien de florins Alicia possédait-elle ?
84. Damier d’Emma
Emma a numéroté cinq cases d’un damier.
Quelles sont les trois cases dont la somme des numéros est 33 ?
85.
Rectangle d’Élise
Élise découpe six petits carrés de même grandeur et les assemble pour
former une pièce rectangulaire 2
´
3.
Combien de pièces 2
´
3 seront nécessaires pour remplir un rectangle 4 × 12 ?
86. Dés de Bernard
Bernard pose six dés sur une table. La face avant des dés est :
Combien y a-t-il de points en tout sur les faces arrière ?
87. Faux résultat
Alexia a additionné les trois nombres suivants. Malheureusement, le
résultat est faux.
Remplacez deux chiffres par 4 pour que la somme soit 1345.
88.
Santé de Laurie
Laurie place d’abord quatre oranges en un carré sur la table. Elle
entoure ce carré de telle manière que 12 oranges forment la première
couronne.
Combien d’oranges Laurie pourra-t-elle placer dans la deuxième
couronne ?
89. Perles de Bruno
Bruno prend le collier de sa mère qui contient 24 perles. Il le
sectionne en six sections. Aucune section ne dépasse sept perles et
toutes les sections sont de longueur différente.
Dans le tableau, placez les sections de perles de façon qu’il y ait 12
perles dans chaque ligne et 8 perles dans chaque colonne.
90. Casse-tête de Gabrielle
Gabrielle découpe cinq petits carrés de même grandeur et les assemble
pour former la pièce de droite.
Combien de pièces seront nécessaires pour remplir un rectangle 6 × 9 ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
91. Noisettes croquantes
Émilie partage 42 noisettes entre ses trois enfants.
Le premier reçoit deux noisettes de plus que le deuxième.
Le deuxième reçoit une noisette de moins que le troisième.
Combien chacun recevra-t-il de noisettes ?
92. Losanges de Patricia
Patricia a tracé la figure ci-après qui contient trois losanges dont
l’un est partagé en deux parties. Elle soutient que cette figure peut
être tracée sans lever le crayon et sans passer plus d’une fois sur une
même ligne.
Patricia a-t-elle raison ?
93. Monsieur Legris
Monsieur Legris a dessiné la figure ci-après qui est formée de 42 petits
carrés. Il a noirci neuf cases.
Combien y a-t-il de carrés 3 × 3 qui contiennent exactement deux cases
noires ?
94. Jeux de société
Cinq amis se rencontrent pour se consacrer à des jeux de société.
Combien de parties seront jouées si chaque personne affronte une fois
chacune des autres ?
95. Grille d’Eugène
Dans cette grille, Eugène a additionné les quatre nombres inscrits dans
les cases colorées. Leur somme est 33.
Trouvez quatre nombres dont la somme est 52 et qui sont disposés comme
dans l’exemple.
96.
Jetons de Mathilde
Mathilde prépare six jetons et les numérote 1, 3, 4, 5, 7 et 9. Elle
désire placer les jetons sur le tableau ci-après de façon à réaliser une
addition.
97. Visites de Tancrède
Depuis le dimanche 14 mars, oncle Tancrède amène ses neveux en balade
pour visiter des fermes. Cette visite s’est faite tous les dimanches
jusqu’au dernier dimanche de mai.
Combien de visites ont été effectuées avec l’oncle Tancrède ?
98. Simon compte
Simon a écrit les lettres de son prénom dans ce tableau. On peut le lire
en joignant les lettres voisines.
Combien de fois en tout peut-on lire SIMON ?
99. Autobus en rangs
Sept autobus sont disposés en trois rangées de trois autobus.
Déplacez un autobus pour avoir cinq rangées de trois autobus.
100. Promenade étoilée
La nuit dernière, Martin s’est promené dans le ciel et y a recueilli des
étoiles. Il veut les répartir dans neuf astres disposés comme ci-après.
En B, il dépose la moitié moins d’étoiles qu’en A. En C, il en dépose la
moitié moins qu’en B. Dans chaque rangée de trois astres reliée par une
droite, il dépose 12 étoiles. Aucun astre n’a le même nombre d’étoiles.
Combien Martin a-t-il recueilli d’étoiles ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
101. Écart de température
Manon a noté la température en degrés Celsius tout au long d’une
semaine.
Quel est le plus grand écart de température entre un jour et son
après-demain ?
102. Crayons amis
Jean et Paul ont ensemble 16 crayons. Si Jean donne un crayon à Paul,
ils ont le même nombre de crayons.
Combien chacun a-t-il de crayons ?
103. Oranges de Laurie
Pendant cinq jours, Laurie achète quatre oranges de plus par jour. Elle
a acheté 13 oranges de plus pendant les deux derniers jours que pendant
les trois premiers.
Combien Laurie a-t-elle acheté d’oranges le dernier jour ?
104. Expression de Malorie
Malorie a représenté 15 avec cinq 5. Elle a écrit : (55 − 5)
÷
5 + 5.
À l’aide d’opérations simples, représentez 3 avec six 9.
105. Dina et son prénom
Dina a écrit les trois égalités ci-après dans lesquelles les lettres de
son prénom apparaissent. Chaque lettre représente un chiffre différent,
à l’exception de 0.
Quelle est la somme des lettres de DINA ?
106. Somme de Lydia
Lydia veut écrire les chiffres de 1 à 6 chacun une fois dans les cases
colorées. Des indices sont donnés en regard de chaque nombre de deux
chiffres.
Trouvez trois nombres dont la somme est 75.
107. Jetons d’Anthime
Anthime découpe quatre jetons et les numérote comme ci-après. Il accole
les jetons pour former des nombres de quatre chiffres.
4 5 6 7
Combien peut-on former de nombres pairs de quatre chiffres ?
108. Dessin de Léa
Léa a tracé la figure ci-après.
Le point indiqué est commun à exactement quatre segments.
Combien y a-t-il de points qui sont communs à exactement trois segments
?
109. Étoiles d’Alexandre
Alexandre a disposé cinq étoiles en deux rangées de trois étoiles comme
ci-dessous.
Ajoutez deux étoiles pour avoir cinq rangées de trois étoiles chacune.
110. Figures de Samuel Samuel a écrit les deux égalités suivantes dans lesquelles on trouve deux symboles différents. Chaque symbole correspond à un chiffre. ▲ ÷ ■ = 2 ■ + ▲ +
▲ = 15
Quelle est la valeur de chacun des deux symboles ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
111. Frère et sœur
Olivier et Olivia ont ensemble 18 ans.
Quand Olivier avait 3 ans, Olivia avait 7 ans.
Quel est l’âge de chacun ?
112. Cure-dents de Nicolas
Nicolas a écrit les chiffres pairs avec des cure-dents comme
ci-dessous ; puis il forme tous les nombres de deux chiffres différents.
Parmi les nombres formés, quel est le plus petit qui exige 10 segments
pour son écriture ?
113. Lettres de Stella
Stella a donné une valeur numérique à cinq lettres. Elle veut former un
mot de quatre lettres dont la valeur est 14 et qui fait rêver.
L = 2 I =
4 E
= 3 T = 6
C = 5
Quel est ce mot ?
114. Symboles de Gabrielle
Gabrielle a écrit deux égalités dans lesquelles elle a introduit les
symboles
x
et
y.
Chaque symbole représente un chiffre différent.
x
+
x
=
y
x
+
y
= 9
Que vaut
y
?
115. Martin Martin
Le nom de famille de Martin est Martin. Son prof de mathématiques
l’appelle parfois Martin au carré : ce qui l’irrite. Martin a écrit
ceci :
M A R T I N M A R T I N M A R T I N ...
Il continue jusqu’à ce qu’il ait écrit la 100e lettre. Quelle
est cette lettre ?
116. Cachette de Manon
Manon a dessiné la figure suivante dans laquelle une case est numérotée
1. Elle veut placer un chiffre par case pour qu’en suivant les lignes on
puisse lire quatre nombres : 1234, 4352, 8716 et 3162.
Complétez la figure.
117. Grille d’Aurélia
Aurélia prépare une grille 3 × 3. La somme des nombres doit être
identique dans chaque ligne, colonne et diagonale. Les nombres de la
première ligne sont 4, 9 et 20. Les nombres de la troisième colonne sont
6, 9 et 18.
Remplissez la grille.
118. Numéro de repère
Le numéro d’identification personnelle de Donald apparaît parmi les
suivants :
827 054
845 414
751 157
912 743
631 736
825 437
• La somme des chiffres est 26.
• La somme du premier et du dernier chiffre est 12.
• Le premier chiffre est plus grand que le dernier.
• La somme des deux chiffres du milieu est 9.
• Le deuxième chiffre est plus petit que le cinquième.
Quel est le numéro de Donald ?
119. Triangles de Charlotte
Charlotte a tracé un triangle. Puis, elle a introduit deux droites
perpendiculaires l’une à l’autre.
Combien peut-on compter de triangles de toute grandeur dans ce dessin ?
120. Combinaisons de Rébecca
Rébecca écrit cinq nombres. À l’aide d’opérations simples, elle essaie
de combiner les nombres pour obtenir certains résultats.
Combinez les cinq nombres de façon que le résultat soit 100. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Solutions 121 à 140
Antoine a assemblé des petits carrés comme ci-après. Il demande à un ami
de partager cette figure en trois parties de même forme et de même
grandeur.
Faites le partage.
122. Fierté de parents
Benjamin et Amélia sont fiers de leurs trois filles.
Leurs noms sont Livia, Lydia et Sophia.
Le produit de leur âge est 45.
Sophia est la plus vieille.
Quel est l’âge de chacune ?
123. Des contes québécois
Depuis sa tendre enfance, Sylvie lit des livres de contes et légendes de
différents pays. Cela lui a donné l’idée d’écrire des contes québécois
où les loups garou et les feux follets côtoient les magiciens modernes.
Elle présente 96 contes à son éditeur. Celui-ci lui dit : « Je voudrais
partager le livre en parties égales, soit en au moins quatre parties et
au moins six contes par partie. »
Combien y a-t-il de possibilités de partage ?
124. Polygones de Léon
Léon a écrit deux égalités en utilisant deux figures distinctes. Chaque
figure représente un chiffre différent. Chaque groupe de deux figures
accolées correspond à un nombre de deux chiffres.
Quelle est la valeur de chacune des deux figures ?
125. Calculs de Micheline
Micheline veut placer les chiffres de 1 à 6 une seule fois dans chacune
des cases de façon que la somme soit 129. Le troisième nombre est
supérieur de 19 au premier et supérieur de 5 au deuxième.
Quels sont ces trois nombres ?
126. Triangle réduit
Nicolas a tracé la figure ci-après dans laquelle il a distribué sept
cellules. Il veut disposer chaque nombre de 1 à 7 pour que la somme soit
12 dans chacune des cinq rangées de trois cellules reliées par une
droite. Le 7 est en bonne position.
Trouvez une façon de distribuer les nombres.
127. Toutous de Léonie
Léonie a 76 toutous qu’elle a distribués dans deux boîtes. La première
boîte contient au moins 18 toutous qui doivent être donnés à six enfants
sans qu’il en reste. La seconde boîte contient au moins 21 toutous qui
doivent être donnés à sept enfants sans qu’il en reste.
Combien y a-t-il de toutous par boîte ?
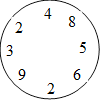
128. Cadran de Claire
Claire a écrit des nombres dans le cadran ci-après.
Partagez le cadran en trois parties de façon que la somme des nombres de
chaque partie soit trois nombres consécutifs.
129. Portraits de Joachim
Joachim a représenté 100 avec cinq 4 et deux 8 comme ceci :
44 + 44 + 8 + 8 – 4
Représentez 100 avec trois 2 et trois 3 en utilisant l’addition et la
multiplication.
130. Nombres de Mélanie
Mélanie écrit tous les nombres de quatre chiffres différents en
utilisant ces chiffres.
3
4
5
6
Combien Mélanie a-t-elle écrit de nombres qui commencent par 6 ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
131. Poussins de Lucas
Lucas a acheté des poussins pour en faire l’élevage. Il les distribue
dans les huit cellules ci-après. Il veut placer respectivement 2, 3, 4,
5, 6, 7, 8 et 10 poussins par cellule. La cellule du coin inférieur
gauche doit recevoir 4 poussins.
Répartissez les autres poussins pour qu’il y en ait 15 dans chaque
rangée horizontale et dans chaque rangée verticale de deux ou de trois
cellules.
132. Refuges d’oiseaux
Il est de ces personnes qui ont un faible pour les oiseaux.
Gilles et Lucie ont construit 11 cabanes d’oiseaux.
Lucie et Carol ont construit 15 cabanes d’oiseaux.
Gilles et Carol ont construit 14 cabanes d’oiseaux.
En tout, combien ces trois personnes ont-elles construit de cabanes
d’oiseaux ?
133. Pensum de Rébecca
Rébecca s’exerce à écrire les nombres en lettres. Il y a un nombre
inférieur à 100 qu’elle n’aime pas car elle trouve qu’il a le plus de
lettres.
Quel est ce nombre ?
134. Lettres monnayables
Sur une planète, les lettres valent des écus. Chaque écu est représenté
par le symbole
Y.
l
A vaut
YY
écus.
l
E vaut
YYY
écus.
l
G vaut
YYYY
écus.
l
R vaut
YYYYY
écus.
Trouvez un mot de six lettres qui utilise uniquement les lettres données
et qui vaut 20 écus.
135.
Cercles de Marielle
Marielle adore la géométrie. Pendant ces temps libres, elle s’exerce à
réaliser des cercles sans compas. Elle décide de tracer trois traits
droits dans un cercle.
Quel est le plus grand nombre de parties que Marielle peut obtenir ?
136. Trophées de Nicolas
Nicolas a disposé cinq trophées en deux rangées de trois trophées
chacune comme ci-dessous.
Ajoutez trois trophées pour avoir six rangées de trois trophées chacune.
137. Timbres d’Armande
Armande a un album qui contient 126 timbres qu’elle donne à son frère.
Celui-ci veut partager les timbres en deux albums tels que l'un contient
les trois quarts de l'autre.
Combien y aurait--il de timbres par album ?
138. Tableau de Nicolas
Nicolas a préparé le tableau ci-après qui contient trois égalités. Il y
a écrit les chiffres 8 et 9.
Dans les cases, écrivez chacun des chiffres de 1 à 7 pour que les trois
égalités soient vraies.
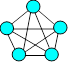
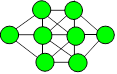
139. Liens de Jérémie
Jérémie a dessiné la figure ci-après dans laquelle il a tracé huit
cercles qui sont reliés les uns aux autres.
Combien y a-t-il de cercles qui sont reliés exactement à quatre cercles
dans cette figure ?
140. Arbres de Vivien
Dix arbres disposés en ligne droite sont à trois mètres l’un de l’autre.
Vivien touche au deuxième, puis au quatrième. Il revient toucher au
premier puis enfin au dixième.
● ●
● ●
● ●
● ●
● ●
Quelle distance Vivien a-t-il parcouru du point de départ au point d’arrivée ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Solutions 141 à 150
Lucas veut placer un signe +, –, × ou ÷ entre chacun des chiffres sans
en changer l’ordre. Le résultat doit être 4.
Insérez les signes appropriés.
142. Alphabet de Jacquelin
Jacquelin écrit les chiffres de 0 à 9 en lettres.
ZÉRO
UN
DEUX
TROIS ...
Combien de lettres de l’alphabet ne seront pas utilisées ?
143. Magie d’Isaac
Isaac a préparé le tableau ci-après. Il veut y placer chacun des nombres
de 1 à 9 de façon que la somme soit 15 dans chaque rangée de deux ou de
trois cellules reliées par une droite. Le 5 et le 9 sont en bonne
position.
144. Souper ensoleillé
C’est un samedi de juillet fort coloré.
Papa Bertrand décide de servir des saucisses à ses rejetons.
Cela lui prend six minutes pour rôtir six saucisses.
Combien de temps cela lui prendra-t-il pour rôtir 12 saucisses ?
145. Bloc-notes de Mélanie
En attendant un courriel, Mélanie sort son bloc-notes et écrit les
chiffres ci-après. Elle assemble les chiffres pour former des nombres de
trois chiffres différents.
Combien y a-t-il de nombres pairs de trois chiffres différents
inférieurs à 540 ?
146. Monnaie de Manon
Manon a placé 10 pièces de monnaie : 2 au centre et 8 dans la première
couronne.
Combien devra-t-il y avoir de pièces dans la deuxième couronne ?
147. Escalier de Nadia
Nadia a dessiné cette grille qui est formée de 15 petits carrés.
Combien peut-on compter de carrés de quatre cases ?
148. Chats de Zoé
Zoé dessine sept petits chats. Elle les marque : P, Q, R, S, 7, 8, 9.
Elle place dans un sac les quatre chats marqués P, Q, R et S. Dans un
autre sac, elle place les chats 7, 8 et 9. Son ami Martin doit tirer au
hasard un chat dans chaque sac.
Combien y a-t-il de combinaisons possibles de deux chats ?
149. Bâtonnets de Florent
Florent prend 18 bâtonnets. Il les assemble de façon à former six carrés
comme ci-dessous.
Enlevez quatre bâtonnets pour obtenir trois carrés.
150. Trous de Souriante
La souris Souriante a pratiqué des trous dans la structure ci-après pour
se faire un chemin. Elle part de l’extérieur ou de l’intérieur de l’une
des trois pièces. Elle doit passer dans chaque trou une seule fois.
De quel endroit Souriante doit-elle partir ?
….. FIN ….. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Solutions | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||