# 7515               18 mars 2026

Légumes de Mireille

Mireille a vendu des paniers de carottes à 30 florins chacun,

puis elle a acheté un sac de pommes de terre.

Il lui reste alors 350 florins.

Si elle avait vendu ses paniers de carottes 20 florins chacun

et acheté le sac de pommes de terre pour la moitié du prix,

il lui resterait 240 florins.

Combien coûte le sac de pommes de terre ? Combien Mireille a-t-elle vendu de sacs de carottes ? >>>  Solution

# 7514               18 mars 2026

Grille de Pauline

Pauline veut placer chacun des nombres de 1 à 49 dans la grille. La somme doit être 175 dans chaque ligne, colonne et diagonale. La somme des deux cases voisines est donnée à l’extérieur de la grille pour chaque rangée, y compris pour les diagonales. Neuf nombres sont en bonne position.

Complétez la grille.  >>>  Solution

# 7513               18 mars 2026

Faux et vrais mots

Jeannot a écrit 12 lettres dans la grille. Il compose des vrais ou des faux mots de trois lettres en prenant une lettre par ligne.

Combien y a-t-il de vrais ou de faux mots qui contiennent chacun une seule voyelle ? >>>  Solution

# 7512               18 mars 2026

Additions de Roger

Roger veut placer chacun des nombres de 1 à 12 dans la figure formée de quatre additions. Quatre nombres sont en bonne position.

Trouvez une façon de compléter la figure. >>>  Solution

# 7511               18 mars 2026

Trèfles de Roland

Roland a écrit l’égalité ci-après. On y trouve cinq trèfles qui prennent chacun des valeurs différentes de 1 à 5. Deux trèfles accolés forment un nombre de deux chiffres.

§ § × § + §§ = 84

Attribuez des chiffres aux trèfles pour que l’égalité soit vraie. >>>  Solution

# 7490               11 février 2026

Magie de Christiane

Christiane a composé un carré magique d’ordre 5. La somme des lignes, des colonnes et des deux diagonales est 65. Les nombres extérieurs sont la somme des deux cases voisines.

Retrouvez le carré magique. >>>  Solution

# 7489               11 février 2026

Double partage de dominos

Dans un sac, il y a entre 66 et 83 dominos.

Lucienne partage également les dominos entre trois équipes.

Les dominos restants sont placés dans une boîte.

Puis, chaque équipe de quatre enfants partage également ses dominos

et place les dominos restants dans la boîte.

Celle-ci contient maintenant cinq dominos.

Combien y avait-il de dominos dans le sac au départ ? >>>  Solution

# 7488               11 février 2026

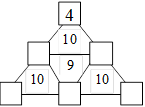
Triangles d’Émilienne

Émilienne veut écrire chacun des nombres de 1 à 6 dans la figure. À l’intérieur de chacun des quatre petits triangles, elle a indiqué la somme des nombres qui devraient apparaître dans les trois cases des sommets. Le 4 est en bonne position.

Complétez la figure. >>>  Solution

# 7487               11 février 2026

Grille d’Éliane

Éliane a écrit des lettres dans cette grille. Chaque lettre représente un chiffre différent. La somme de chaque ligne et de chaque colonne doit être 18. On sait que A = 5, B = 6 et G = 9. De plus, aucune lettre ne vaut 8.

Remplissez la grille avec des chiffres. >>>  Solution

# 7486               11 février 2026

Recherche de Thomas

Thomas est entré à l’université un mercredi 8 septembre.

Il a présenté son premier travail de recherche

le 8 décembre suivant.

Quel était alors le jour de la semaine ? >>>  Solution