|
(Dessin réalisé au primaire) Contactez-moi : cejean@charleries.net |
Les charleries Bienvenue sur mon blogue, Ce blogue contient des souvenirs, des anecdotes, des opinions, de la fiction, des bribes d’histoire, des récréations et des documents d’archives. Charles-É. Jean
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Propos mathématiques |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6235
21 janvier 2022
Chemins de grilles
Problème.
Combien y a-t-il de chemins pour se rendre dans la case du coin
inférieur droit d’une grille carrée si on part de la case du coin
supérieur gauche et si on procède toujours de gauche à droite et de
haut en bas sans jamais revenir en arrière ?
Solution. Dans une grille 1 × 1, il y a un seul chemin. Dans une
grille 2 × 2, on compte 2 chemins.
Une grille 3 × 3
Dans une telle grille, il y a 6 chemins différents. Les voici :
Une grille 4 × 4
Dans cette grille, on compte 20 chemins.
Une grille 5 × 5
Dans cette grille, on compte 70 chemins : 35 en passant par la case
2 de la première ligne et 35 en passant par la case 2 de la deuxième
ligne.
On peut entrer les données dans ce tableau.
Cas général
Le nombre de chemins peut être décomposé ainsi :
2 × 2 : 1 × 2 = 2
3 × 3 : (1 + 2)2 = 6 4 × 4 : (1 + 3 + 6)2 = 20
5 × 5 : (1 + 4 + 10 + 20)2 = 70
6 × 6 : (1 + 5 + 15 + 35 + 70)2 = 252
Par exemple, pour passer de 5 × 5 à 6 × 6, on fait :
1 + 4 = 5
1 + 4 + 10 = 15
1 + 4 + 10 + 20
= 35
1 + 4 + 10 + 20
+ 35 = 70
(1 + 5 + 15 + 35 + 70)2
= 252
Le terme général est (2n – 2)!/[(n – 1)!]2.
Si n = 5, on a : (8)!/(4!)2
= 70.
Si n = 6, on a (10)!/(5!)2 = 252.
La suite est : 1, 2, 6, 20, 70, 252, 924,
3432, 12 870, 48 620, 184 756, 705 432, … On voit que la croissance
est très rapide.
Ces données se trouvent en colonne centrale dans le triangle de Pascal.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6200
30 décembre 2021
Sommes de
cubes (2)
Il est possible de trouver des égalités de cubes à
partir d’un tableau. Par exemple, on écrit en abscisse les cubes de
1 à 14 et en ordonnée les cubes de 1 à 13. On remplit le tableau en
effectuant les sommes.
Avec les nombres qui apparaissent dans ce tableau,
on écrit des égalités comportant autant de termes que l’on veut.
Sous chaque terme de l’égalité, on écrit les deux cubes qu’on trouve
dans le tableau. Par exemple, 73 + 113 = 1674.
Voici des exemples de sommes qu’on associe aux
cubes :
Quatre cubes
•
1216 + 512 = 1728
63 + 83 + 103 = 123
•
1 + 1728 = 1729
13 + 123 = 93 + 103
Cinq cubes
•
1729 + 468 = 2197
13 + 53 + 73 + 123
= 133
•
2205 + 539 = 2744
23 + 33 + 83 + 133
= 143
Six cubes
•
28 + 526 + 125 = 729
13 + 33 + 43 + 83
+ 53 = 93
Sept cubes
•
559 + 513 = 72 + 1000
13 + 63 + 73 + 83
= 23 + 43 + 103
•
1001 + 737 = 407 + 1331 = 1738
13 + 23 + 93 + 103
= 43 + 73 + 113
Huit cubes
•
2745 + 855 = 2205 + 1395 = 3600 = 602
13 + 73 + 83 + 143
= 23 + 43 + 113 + 133
On peut additionner ou soustraire tout nombre à
chaque base, on obtient d’autres égalités. Par exemple, si on
additionne 1, on a :
23 + 83 + 93 + 153
= 33 + 53 + 123 + 143
•
1729 + 152 + 64 = 945 + 1000
13 + 123 + 33 + 53
+ 43 = 63 + 93 + 103
Neuf cubes
•
1736 + 1343 + 729 = 2261 + 1547 = 3808
23 + 73 + 93 + 103
+ 123 = 43 + 63 + 113 +
133
Dix cubes
•
28 + 468 + 3256 = 224 + 3528 = 3752 13 + 33 + 53 + 73 + 83 + 143 = 23 + 63 + 113 + 133 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6170
12 décembre 2021
Polygonaux et suites
Un nombre
polygonal est un nombre qui peut être représenté par un polygone
régulier constitué de points disposés de façon symétrique. Voici
quatre ordres de polygonaux :
Nous allons tenter de trouver des égalités de
polygonaux en appliquant
la théorie des suites.
Égalité de six polygonaux du
même ordre
On forme une suite de quatre
termes qui commence par 3 et dont la raison est 2. On additionne 8 à
chacun des termes. On munit chaque terme d’un exposant relatif aux
nombres polygonaux. On colorie les cases ainsi :
Le
premier membre de l’égalité peut être formé par les nombres d’une
couleur. Le deuxième membre l’est alors par les nombres de l’autre
couleur.
En considérant les triangulaires dont l’exposant est Δ, on peut
écrire :
5Δ + 13Δ + 15Δ = 7Δ
+ 9Δ + 17Δ = 226
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Égalité de huit polygonaux du même ordre
Cas 1. On forme une suite de
quatre termes qui commence par 5 et dont la raison est 2. On
additionne 3 à chacun des termes. On colorie les cases ainsi :
Le
premier membre de l’égalité peut être formé par les nombres d’une
couleur. Le deuxième membre l’est alors par les nombres de l’autre
couleur. En considérant les carrés, on peut écrire en ordre
numérique :
52 + 102 + 112 +
122 = 72 + 82 + 92 + 142
= 390
Cette égalité est vraie pour les polygonaux de tout
ordre.
Cas 2. On écrit une
suite de 8 termes qui commence par 2 et dont la raison est 3. On
additionne 24 à chacun des termes.
En considérant les pentagonaux
dont l’exposant est p, on peut écrire :
2p + 23p
+ 35p + 38p = 11p + 14p
+ 26p + 47p = 4754
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Cas 3. Avec les mêmes
suites, on peut colorer les cases d’une façon différente.
En considérant les hexagonaux
dont l’exposant est h, on peut écrire :
5h + 20h
+ 32h + 41h = 8h + 17h +
29h + 44h = 6162
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Égalité de 10 polygonaux du
même ordre
Sur la première ligne,
on écrit une suite. Sur la deuxième ligne, on commence l’autre suite
avec le sixième terme de la suite précédente. On applique la même
raison dans les deux cas.
Après avoir supprimé les
doublons de part et d’autre, en considérant les triangulaires, on
obtient :
1Δ
+ 7Δ
+ 25Δ
+ 28Δ
+ 34Δ
= 4Δ
+ 10Δ
+ 13Δ
+ 31Δ
+ 37Δ
= 1355
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Égalité de 12 polygonaux du
même ordre
Sur la première ligne,
on écrit une suite. Sur la deuxième ligne, on commence l’autre suite
avec le dernier terme de la suite précédente. On applique la même
raison.
En considérant les carrés, on
obtient :
12 + 132
+ 162 + 222 + 342 + 372
= 42 + 72 + 192 + 252 +
282 + 402 = 3435
Cette égalité est vraie pour les polygonaux de tout
ordre.
Égalité de 14 polygonaux du
même ordre
Cas 1. Sur la première
ligne, on écrit une suite. Sur la deuxième ligne, on commence
l’autre suite avec le dernier terme de la suite précédente. On
applique la même raison.
Après avoir supprimé les
doublons de part et d’autre et en considérant les pentagonaux, on
obtient :
1p + 7p
+ 16p + 25p + 31p + 34p
+ 40p = 4p + 10p + 13p +
19p + 28p + 37p + 43p =
6895
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Cas 2. Sur la première
ligne, on écrit les nombres de 1 à 7. On additionne 8 à chaque
nombre.
En considérant les hexagonaux,
on obtient :
1h + 2h
+ 7h + 10h + 11h + 12h +
13h = 3h + 4h + 5h + 6h
+ 9h + 14h + 15h
= 1120
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Égalité de 16 polygonaux du même ordre
On écrit sur la première ligne les nombres de 2 à 9. On additionne
8 à ces nombres.
En
considérant les hexagonaux, on peut écrire :
2h + 5h + 6h + 9h + 11h
+ 12h + 15h + 16h = 3h +
4h + 7h + 8h + 10h + 13h
+ 14h + 17h = 1708
Cette égalité est vraie pour les polygonaux de tout
ordre y compris les carrés.
Voici d’autres rectangles qui
peuvent générer des égalités de polygonaux de tout ordre y compris
les carrés :
Cas 1.
Cas 2.
Cas 3.
Dans ce dernier cas, si on
attribue à chaque terme l’exposant 3, on obtient une égalité de
cubes. 23 + 53 + 73 + 83 + 123 + 133 + 153 + 183 = 33 + 43 + 63 + 93 + 113 + 143 + 163 + 173 = 14 120 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6145 27 novembre 2021
Quatre cubes
L’algèbre peut être un outil très
efficace pour trouver des égalités de cubes. Nous allons expliquer
trois cas où l’égalité est de la forme p3 + q3
= r3 + s3. Cette égalité peut aussi être de la
forme p3 + q3 + r3 = s3
ou toute forme de quatre cubes dont la valeur est positive ou
négative.
1. Formule des trinômes
Une formule consiste à choisir
arbitrairement la valeur de deux entiers a et b et à
remplacer ces deux entiers dans chacune des quatre égalités
suivantes :
x
= 28a2
+ 11ab - 3b2
y = 21a2 - 11ab - 4b2
Si a = 1 et b = 1, on obtient : x =
36, y = 6, z = 48, u = 54. On peut écrire :
363 + 63 + 483
= 543
Lorsque les quatre nombres ont un
facteur commun, on peut simplifier en divisant chacun des nombres
par le facteur commun. On obtient :
63 + 13 + 83
= 93
Si a = 1 et b = 2, on obtient : x =
38, y = -17, z = 73, u = 76. On peut écrire :
383 – 173 +
733 = 763
Si on veut éliminer le signe –, on
transporte 173 dans l’autre membre. Cela donne :
383 + 733 =
173 + 763
Si a = 2 et b = 1, on obtient : x =
131, y = 58, z = 160, u = 187. On peut écrire :
1313 + 583 +
1603 = 1873
Si a = 0 et b = 1, on obtient : x =
-3, y = -4, z = 6, u = 5. On peut écrire :
-33 - 43 + 63
= 53
33 + 43 + 53
= 63
Si a = 1 et b = 0, on obtient : x =
28, y = 21, z = 35, u = 42. On peut écrire :
283 + 213 +
353 = 423
2. Formule avec neuf variables
On choisit arbitrairement deux
nombres qu’on appelle a et b.
• On fait : c = a2 + 3b2.
• On fait : d = a + 3b.
• On fait : e = a – 3b.
• On fait : p = cd – 1.
• On fait : q = c2 – d.
• On fait : r = c2 – e.
• On fait : s = ce – 1.
• On écrit
p3
+ q3 = r3 + s3.
Soit a = 2 et b = 1. Alors, c = 7,
d = 5, e = -1, p = 34, q = 44, r = 50, s = -8. L’égalité est :
343 + 443 =
503 – 83 = 124 488.
Pour éliminer le nombre négatif, on
le transporte dans le premier membre. On peut écrire :
83 + 343 + 443
= 503.
À partir de cette égalité, on peut
trouver celle qui est primitive, c’est-à-dire celle dont les termes
n’ont pas de facteur commun. Dans ce cas-ci, on divise par 2. On
obtient :
43 + 173 + 223
= 253
On pourrait encore diviser par 2.
L’égalité est encore vraie, mais on a deux nombres décimaux :
23 + 8,53 +
113 = 12,53
De façon générale, on peut
multiplier ou diviser chacun des termes et les égalités sont
toujours vraies.
Un autre exemple. Soit a = 4 et b =
1. Alors, c = 19, d = 7, e = 1, p = 132, q = 354, r = 360, s = 18.
L’égalité est :
1323 + 3543 =
3603 + 183 = 46 661 832
L’égalité primitive correspondante
est :
223 + 593 =
603 + 33 = 216 027
Fait surprenant : 216 est le cube
de 6 et 027 est le cube de 03, comme dans 603.
3. Autre formule avec neuf
variables
On choisit deux nombres qu’on
appelle a et b.
• On fait : c = 7a2.
• On fait : d = ab.
• On fait : e = b2.
• On fait : p = 4c + 11d – 3e.
• On fait : q = 3c – 11d – 4e.
• On fait : r = -(5c + 7d + 6e).
• On fait : s = 6c + 7d + 5e.
• On écrit
p3
+ q3 = r3 + s3.
Soit a = 1 et b = 1. Alors, c = 4,
d = 1, e = 1, p = 36, q = 6, r = 48, s = 54. On peut écrire :
363 + 63 =
-483 + 543 = 46 872
Après avoir transféré 483
dans le premier membre, on a :
63 + 363 + 483
= 543.
L’égalité primitive est :
13 + 63 + 83
= 93
Un autre exemple. Soit a = 2 et b =
1. Alors, c = 28, d = 2, e = 1, p = 131, q = 58, r = -160, s = 187.
On peut écrire : 1313 + 583 = -1603 + 1873 ou encore 1313 + 583 + 1603 = 1873. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6115
9 novembre 2021
Dons de caramels
Dans ces problèmes, on veut savoir
combien chacun a de caramels après avoir fait des hypothèses de
dons. Des démarches sont données.
Problème 1
France dit à Gratien :
« Si tu me donnais 10 de tes caramels, j’en aurais le double de
toi ».
Gratien reprend :
« Si tu me donnais 8 de tes caramels, j’en aurais le double de
toi ».
Combien chacun a-t-il de caramels ?
Stratégie 1. Utilisation de tableaux
On suppose que France a 2 caramels.
Selon ses dires, Gratien en aura 16. Si France a 4 caramels, Gratien
en aura 17. Si France a 6 caramels, Gratien en aura 18, etc. On
écrit les données dans le tableau.
On suppose que Gratien a 2
caramels. Selon ses dires, France en aura 13. Si Gratien a 4
caramels, France en aura 14. Si Gratien a 6 caramels, France en aura
15, etc.
Dans le premier tableau, on note
que les nombres attribués à France augmentent de 2. Ceux attribués à
Gratien augmentent de 1. Dans le second tableau, c’est l’opposé qui
se produit. On arrête d’écrire les données dans les tableaux quand
on aperçoit les deux mêmes nombres d’un tableau à l’autre dans une
colonne.
France a 26 caramels et Gratien en a 28.
Stratégie 2. À l’aide de l’algèbre
France a x caramels. Elle en reçoit
10 de Gratien. Elle en a (x + 10). Gratien a y caramels. Il en donne
10 à France. Il en a (y – 10). Comme France en a le double de
Gratien, pour avoir une égalité, il faut multiplier par 2 l’avoir de
Gratien. L’équation est : x + 10 = 2(y – 10).
On fait le même raisonnement
concernant les paroles de Gratien. L’équation est : 2(x – 8) = y +
8. On résout les deux équations. On trouve x = 26 et y = 28.
France a 26 caramels et Gratien en a 28.
Stratégie 3. On généralise
Soit x le nombre de caramels de
France et y celui de Gratien. Soit f le don de France et g le don de
Gratien. On peut écrire : x + g = 2(y – g) et 2(x – f) = y + f. On
résout les deux équations. On obtient : x = 2f + g et y = f + 2g.
Or, f = 8 et g = 10. D’où, x = 26 et y = 28. France a 26 caramels
et Gratien en a 28.
Problème 2
France dit à Gratien :
« Si tu me donnais 15 de tes caramels, j’en aurais le double de
toi ».
Gratien reprend :
« Si tu me donnais 11 de tes caramels, j’en aurais le double de
toi ».
Combien chacun a-t-il de caramels ?
Maintenant qu’on est plus familier avec ce genre de problèmes, on
peut trouver d’autres stratégies. En voici quatre pour ce problème :
Stratégie 1
• On additionne le don de Gratien et deux fois le don de France :
c’est l’avoir de France.
• On additionne le don de France et deux fois le don de Gratien :
c’est l’avoir de Gratien.
On fait : 15 + 2 × 11 = 37, puis 11 + 2 × 15 = 41. France a 37
caramels et Gratien en a 41.
Stratégie 2
• On additionne les dons.
• On multiplie par 2.
• Du résultat, on soustrait le don de Gratien : c’est l’avoir de
France.
• Du résultat, on soustrait le don de France: c’est l’avoir de
Gratien.
On fait : 15 + 11 = 26, 26 × 2 = 52, 52 – 15 = 37 et 52 – 11 = 41.
France a 37 caramels et Gratien en a 41.
Stratégie 3
• On additionne les dons.
• On multiplie par 1,5.
• On soustrait la moitié de la différence des dons : c’est l’avoir
de France.
• On additionne la moitié de la différence des dons : c’est l’avoir
de Gratien.
On fait : 15 + 11 = 26, 26 × 1,5 = 39, 15 – 11 = 4, 4 ÷ 2 = 2, 39 –
2 = 37 et 39 + 2 = 41. France a 37 caramels et Gratien en a 41.
Stratégie 4
On additionne les dons et on multiplie par 3. On fait : 15 + 11 =
26 et 26 × 3 = 78. On soustrait les dons. On fait : 15 – 11 = 4. Il
s’agit de trouver deux nombres dont la somme est 78 et dont la
différence est 4.
France a 37 caramels et Gratien en a 41. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6085
21 octobre 2021
Sommes de cubes (1)
Il est
relativement facile de trouver des égalités de carrés.
Nous allons présenter quatre
formules différentes qui permettent de trouver des égalités de
cubes.
4.1 Formule d’Euler
Euler a fourni une formule pour
trouver des égalités de quatre cubes de la forme x3 + y3
= z3 + u3. Nous avons transformé cette formule
en un algorithme. On procède ainsi :
Étapes
• On attribue une valeur à une
variable a et à une variable b.
• On fait : p = a2 + 3b2,
q = a + 3b et r = a – 3b.
• On fait x = pq – 1, y = p2
– q, z = p2 – r, u = pr – 1.
• Si un résultat est négatif, on le
transfère dans l’autre membre.
Exemple 1. On pose a = 1 et b = 2.
Alors, p = 13, q = 7 et r = -5. Pour les autres variables, on a : x
= 90, y = 162, z = 174 et u = -66. Après avoir transféré 66 dans le
premier membre, on peut écrire :
663 +
903
+ 1623 = 1743 =
5 268 024
Exemple 2. On pose a = 2 et b = -2.
Alors, p = 16, q = -4 et r = 8, puis x = -65, y = 260, z = 248 et u
= 127. On peut écrire :
653 + 1273
+ 2483 = 2603 =
17 576 000
4.2 Formule de Rebout
Dans les Nouvelles annales de mathématiques, Eugène Rebout a
publié un court article intitulé
Formation d'un cube entier qui soit égal à la somme de quatre cubes
entiers.
Les égalités sont de la
forme p3 = q3 + r3 + s3
+ t3. Voici l’algorithme :
• On donne des valeurs à a, b et c telles que 3abc est un cube.
• On remplace chaque variable par sa valeur :
p = a + b + c,
q = a + b – c,
r = a – b + c,
s = b + c – a.
t est la racine cubique de 24abc.
• On place p dans le premier membre avec, s’il y a lieu, les
résultats négatifs.
Soit a = 4, b = 6 et c = 3. Alors, p = 13, q = 7, r = 1, s = 5 et t
= 12. On a :
133 = 13 + 53 + 73 + 123
= 2197
Soit a = 2, b = 3 et c = 12. Alors, p =17, q = -7, r = 11, s = 13 et
t = 12. Après le transfert du 7 dans le premier membre, on peut
écrire :
173 + 73 = 113 + 123 +
133 = 5256.
4.3 Nouvelle formule (1)
•
p = a2
•
q = 2a2 – 3a + 3
•
r = a3 – q
•
s = r + 3
On
écrit sous la forme p3 + q3 + r3 =
s3.
Si a = 5, alors p = 25, q = 38, r = 87, s = 90. On obtient
l’égalité :
253 + 383 + 873 = 903 =
729 000.
•
On donne une valeur à a et on déduit la valeur des autres variables.
• p = a2
•
q = 2a2 + 3a + 3
•
r = a3 + q – 3
•
s = r + 3
On
écrit sous la forme p3 + q3 + r3 =
s3.
Si a = 5, alors p = 25, q = 68, r = 190, s = 193. On obtient
l’égalité :
253 + 683 + 1903 = 1933
= 7 189 057. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6055
3 octobre 2021
Polygonaux et sommes
Un nombre
polygonal est un nombre qui peut être représenté par un polygone
régulier constitué de points disposés de façon symétrique. Voici
quatre ordres de polygonaux :
Nous allons tenter de trouver des égalités de
polygonaux en additionnant des bases de même somme ou en combinant
des bases de sommes différentes.
Une même somme
On choisit un nombre qui sera la somme des bases
avec les triangulaires. On établit la somme de tous les couples de
triangulaires dont la somme des bases est ce nombre. Par exemple, on
choisit 19.
Égalité de huit polygonaux du même ordre
On recherche deux sommes dont la somme est la même
que celle d’un autre couple de sommes. Dans ce cas-ci, les
possibilités sont :
172 + 100 = 142 + 130 = 272
156 + 106 = 142 + 120 = 262
142 + 100 = 130 + 112 = 242
130 + 102 = 120 + 112 = 232
On écrit les deux éléments qui composent chaque
somme. Voici l’égalité pour chaque possibilité en considérant les
carrés :
12 + 92 + 102 + 182
= 32 + 42 + 152 + 162 =
506
22 + 72 + 122 + 172
= 32 + 52 + 142 + 162 =
486
32 + 92 + 102 + 162
= 42 + 62 + 132 + 152 =
446
42 + 82 + 112 + 152
= 52 + 62 + 132 + 142 =
426
Ces égalités
valent pour les polygonaux de tout ordre. Cela est aussi vrai pour
les cubes.
13 + 93 + 103 + 183
= 33 + 43 + 153 + 163 =
7562
Égalité de 12 polygonaux du même ordre
Dans le tableau, on recherche trois sommes dont la
somme est la même que celle d’un autre triplet de sommes.
Par exemple, on écrit : 172 + 106 + 100 = 156 + 120
+ 102 = 378. Voici l’égalité en considérant les nombres
pentagonaux dont l’exposant est p :
1P + 7P + 9P + 10P
+ 12P + 18P = 2P + 5P +
8P + 11P + 14P + 17P =
1020
Cette
égalité est vraie pour les polygonaux de tout ordre. Elle est vraie
aussi pour les cubes.
13 + 73 + 93 + 103
+ 123 + 183 = 23 + 53 +
83 + 113 + 143 + 173 =
9633
Égalité de 16 polygonaux du même ordre
Dans le tableau, on recherche quatre sommes dont la
somme est la même que celle d’un autre quadruplet de sommes.
Par exemple, on écrit : 172 + 130 + 106 + 102 = 156
+ 142 + 112 + 100 = 510. Voici l’égalité en considérant les
triangulaires :
1Δ + 4Δ + 7Δ + 8Δ
+ 11Δ + 12Δ + 15Δ + 18Δ
= 2Δ + 3Δ + 6Δ + 9Δ + 10Δ
+ 13Δ + 16Δ + 17Δ = 510
Cette égalité est vraie pour les polygonaux de tout
ordre. Elle s’applique aussi aux cubes.
13 + 43 + 73 + 83
+ 113 + 123 + 153 + 183
= 23 + 33 + 63 + 93 + 103
+ 133 + 163 + 173 = 13 186
Des sommes combinées
On choisit deux nombres qui seront la somme de
bases. Pour chacun, on établit la somme de tous les couples de
triangulaires. Par exemple, on choisit 9 et 13.
Égalité de six polygonaux du même ordre
À partir du tableau, on peut écrire : 37 + 49 = 31
+ 55. On écrit les deux éléments qui composent chaque somme. Voici
une égalité en considérant les pentagonaux :
1P + 8P + 6P + 7P
= 2P + 7P + 4P + 9P =
214
On biffe 7P de part et d’autre.
L’égalité est :
1P + 6P + 8P = 2P
+ 4P + 9P = 144
Cette égalité est vraie pour les polygonaux de tout
ordre, y compris pour les carrés.
Égalité de huit polygonaux du même ordre
À partir du même tableau, on peut écrire : 37 + 49
= 25 + 61. On écrit les deux éléments qui composent chaque somme.
1Δ + 8Δ + 6Δ + 7Δ
= 4Δ + 5Δ + 3Δ + 10Δ =
86
En considérant les heptagonaux dont l’exposant est
s, on a l’égalité :
1S + 6S + 7S + 8S
= 3S + 4S + 5S + 10S =
342
Cette égalité est vraie pour les polygonaux de tout ordre, y compris pour les carrés. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6020
12 septembre 2021
Égalités de polygonaux
Un nombre
polygonal est un nombre qui peut être représenté par un polygone
régulier constitué de points disposés de façon symétrique. Voici
quatre ordres de polygonaux :
Un même
nombre peut appartenir à plusieurs ordres de polygonaux. Par
exemple, 45 est à la fois triangulaire et hexagonal.
La notion
de suite arithmétique joue un rôle important dans l’existence de ces
nombres. En effet, ceux-ci sont formés par l’addition des éléments
d’une suite toujours à partir de 1. Voici la distribution pour les
cinq plus petits nombres polygonaux d’ordres 3 à 6 :
Nombres
triangulaires ou d’ordre 3 : suite de raison 1
Nombres
carrés ou d’ordre 4 : suite de raison 2
Nombres
pentagonaux ou d’ordre 5 : suite de raison 3
Nombres
hexagonaux ou d’ordre 6 : suite de raison 4
Par
exemple, pour les nombres hectogonaux ou polygonaux d’ordre 100, le
premier nombre est 1, le deuxième 100 et la raison 98. On aura
donc la suite : 1, 100, 297, 592, 985, etc. En effet, 1 + 99 = 100,
1 + 99 + 197 = 297, 1 + 99 + 197 + 295 = 592, etc.
Nous donnons six propositions
qui s’appliquent lorsqu’une égalité est vraie pour les nombres
polygonaux de tous les ordres. Ces égalités découlent souvent de
carrés magiques.
Proposition 1
On peut
additionner un même nombre à chaque base. On retrouve alors une
nouvelle égalité.
Soit l’égalité
1P + 7P + 10P = 2P + 5P
+ 11P = 216 où p est l’exposant pentagonal.
Par exemple, on additionne 9 à chacune des bases.
On obtient :
10P + 16P + 19P =
11P + 14P + 20P = 1053
Si l’exposant est 2, on écrira : 12 + 72
+ 102 = 22 + 52 + 112 =
150.
En additionnant 9 à chacune des bases, on obtient :
102 + 162 + 192 =
112 + 142 + 202 = 717
Proposition 2
On peut, de chaque
base, soustraire un même nombre. On retrouve alors une nouvelle
égalité. Par exemple, en partant de la dernière égalité, on
soustrait 9. On obtient les égalités de départ.
Il est fort
probable alors que des bases négatives apparaîtront. Pour donner un
exemple avec les triangulaires, il faut savoir que
0Δ = 0, -1Δ = 0, -2Δ
= 1, -3Δ = 3, -4Δ = 6, etc.
Proposition 3
On peut multiplier
chaque base par un même nombre. On retrouve alors une nouvelle
égalité.
Soit l’égalité 2Δ
+ 7Δ
+ 9Δ
= 3Δ
+ 5Δ
+ 10Δ
= 76 où
Δ est l’exposant triangulaire.
Par exemple, on multiplie par 4 chacune des bases.
On obtient :
8Δ
+ 28Δ
+ 36Δ
= 12Δ
+ 20Δ
+ 40Δ
= 1108
Si l’exposant est 2, on écrira : 22 + 72
+ 92 = 32 + 52 + 102 =
134.
En multipliant par 4 chacune des bases, on
obtient :
82 + 282 + 362 =
122 + 202 + 402 = 2144
Proposition 4
On peut diviser
chaque base par un même nombre. On retrouve alors une nouvelle
égalité. Les bases de ces nouvelles égalités seront composées en
grande partie par des nombres fractionnaires. Cela ne rend pas
fausse l’égalité, mais elle manque d’élégance. Par exemple, en
divisant par 8 la dernière égalité de la proposition 3, on obtient :
1 + 3,5 + 4,5 =
1,5 + 2,5 + 5 = 33,5
On peut ajouter un
même chiffre devant chaque base. On retrouve alors une nouvelle
égalité.
Dans ce cas, il
faut considérer que toutes les bases ont le même nombre de chiffres,
quitte à ajouter un ou des 0 devant certains nombres. Par exemple,
dans l’égalité
42 + 82 + 112 + 152 = 52
+ 62 + 132 + 142 = 426, on
considère 4, 8, 5 et 6 comme étant 04, 08, 05 et 06. Si on ajoute 1
au début, on peut écrire :
1042 + 1082 + 1112
+ 1152 = 1052 + 1062 + 1132
+ 1142 = 48 026
Proposition 6
On peut ajouter un
même chiffre après chaque base. On retrouve alors une nouvelle
égalité.
À partir de la
première égalité de la proposition précédente, si on ajoute 1 à la
fin de chaque base, on peut écrire : 412 + 812 + 1112 + 1512 = 512 + 612 + 1312 + 1412 = 43 364 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
5990
12 juin 2021
Des égalités de carrés
On peut trouver
des égalités de carrés en faisant des opérations sur des fractions de
sommes. On procède de la façon suivante :
•
On détermine le nombre n d’entiers qu’on devra choisir.
•
On choisit une somme : cette somme doit tenir compte de
la valeur de n et elle doit être divisible par n/2.
• On choisit les n entiers.
• On divise la somme par n/2.
• Du résultat, on soustrait chacun
des n entiers.
• On élève au carré chaque élément.
• On écrit le carré des éléments
choisis dans le premier membre et, dans l’autre membre, le carré des
éléments déduits.
Six carrés
Cas 1. On choisit
quatre entiers dont l’un est le quart de la somme.
Exemple.
Choisissons 4, 7, 8, 13. La somme est 32. On divise par 2. Le résultat
est 16. En soustrayant de 16, on obtient : 12, 9, 8, 3. On peut écrire :
42 + 72
+ 82 + 132 = 32 + 82 + 92
+ 122 = 298
Comme 82
apparaît dans chaque membre de l’égalité, on le biffe. On a alors :
42 + 72
+ 132 = 32 + 92 + 122 = 234
Cas 2. On choisit
six entiers dont l’un est le sixième de la somme et dont un couple est
le tiers de la somme.
Exemple.
Choisissons 1, 5, 6, 7, 8,
9. La somme est 36. On divise par 3. Le résultat est 12. En soustrayant
de 12, on obtient : 11, 7, 6, 5, 4, 3. Après avoir biffé les doublons de
part et d’autre, on peut écrire :
12 + 82
+ 92 = 32 + 42 + 112 = 146
Huit carrés
Cas 1. On choisit
quatre entiers dont aucun n’est le quart de la somme. De plus,
l’addition d’éléments pris deux à deux ne donne pas la moitié de la
somme.
Exemple 1.
Choisissons 1, 7, 9, 13. La somme est 30. La moitié de la somme est 15.
De 15, on soustrait chacun de ces quatre éléments. On obtient : 14, 8,
6, 2. On peut écrire :
12 + 72
+ 92 + 132 = 22 + 62 + 82
+ 142 = 300
Exemple 2.
Choisissons 3, 5, 9, 21. La somme est 38. La demi-somme est 19. En
soustrayant de 19, on obtient : 16, 14, 10, - 2. On peut écrire :
32 + 52
+ 92 + 212 = 22 + 102 + 142
+ 162 = 556
On aura compris
qu’on accepte les nombres négatifs et, comme le carré d’un nombre
négatif est positif, on peut considérer l’élément comme positif.
Cas 2. On choisit
huit entiers dont quatre appartiennent à des couples dont la somme est
le quart de la somme.
Exemple.
Choisissons 1, 4, 5, 7, 8, 10, 12, 13. La somme est 60. Le quart de la
somme est 15. De 15, on soustrait chacun de ces huit éléments. On
obtient : 14, 11, 10, 8, 7, 5, 3, 2. Après avoir éliminé les doublons,
on peut écrire :
12 + 42
+ 122 + 132 = 22 + 32 + 112
+ 142 = 330
Dix carrés
On choisit six
entiers dont l’un est le sixième de la somme.
Exemple.
Choisissons 2, 3, 7, 8, 9, 13. La somme est 42. Le tiers de la somme est
14. De 14, on soustrait chacun de ces six éléments. On obtient : 12, 11,
7, 6, 5, 1. Après avoir éliminé le doublon, on peut écrire :
22 + 32
+ 82 + 92 + 132 = 12 + 52
+ 62 + 112 + 122 = 327
Douze carrés
Cas 1. On choisit
six entiers. On prend le tiers de la somme. Aucun entier n’est le
sixième de la somme. De plus, l’addition d’éléments pris deux à deux ne
donne pas le tiers de la somme.
Exemple.
Choisissons 2, 4, 8, 12, 13, 15. La somme est 54. Le tiers de la somme
est 18. De 18, on soustrait chacun de ces six éléments. On obtient : 16,
14, 10, 6, 5, 3. On peut écrire :
22 + 42
+ 82 + 122 + 132 + 152 = 32
+ 52 + 62 + 102 + 142 + 162
= 622
Cas 2. On choisit
huit entiers. L’addition d’éléments pris deux à deux donne le quart de
la somme.
Exemple.
Choisissons 2, 3, 8, 9, 11, 12, 13, 18. La somme est 76. Le quart de la
somme est 19. De 19, on soustrait chacun de ces éléments. On obtient :
17, 16, 11, 10, 8, 7, 6, 1. Après avoir biffé deux carrés identiques de
part et d’autre, on peut écrire :
22 + 32
+ 92 + 122 + 132 + 182 = 12
+ 62 + 72 + 102 + 162 + 172
= 731
Quatorze carrés
On choisit huit
entiers. On prend le quart de la somme. Un entier doit être le huitième
de la somme.
Exemple.
Choisissons 3, 5, 8, 12, 14, 15, 17, 22. La somme est 96. Le quart de la
somme est 24. De 24, on soustrait chacun de ces éléments. On obtient :
21, 19, 16, 9, 10, 7, 2. On peut écrire :
32 + 52
+ 82 + 142 + 152 + 172 + 222
= 22 + 72 + 92 + 102 + 162
+ 192 + 212 = 1292
Seize carrés
On choisit huit
entiers. On prend le quart de la somme. Aucun entier n’est le huitième
de la somme. De plus, l’addition d’éléments pris deux à deux ne donne
pas le quart de la somme.
Exemple.
Choisissons 4, 6, 10, 12, 15, 17, 19, 21. La somme est 104. Le quart de
la somme est 26. De 26, on soustrait chacun de ces éléments. On
obtient : 22, 20, 16, 14, 11, 9, 7, 5. On peut écrire :
42 + 62
+ 102 + 122 + 152 + 172 + 192
+ 212 = 52 + 72 + 92 + 112
+ 142 + 162 + 202 + 222 =
1612
On peut
additionner un même nombre à chacune des égalités trouvées dans cet
article. En regard du dernier exemple, quand on additionne 1, on
obtient : 52 + 72 + 112 + 132 + 162 + 182 + 202 + 222 = 62 + 82 + 102 + 122 + 152 + 172 + 212 + 232 = 1828 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5965
27 mai 2021
Magie 4 × 4 et polygonaux
Un nombre
polygonal est un nombre qui peut être représenté par un polygone
régulier constitué de points disposés de façon symétrique. Voici quatre
ordres de polygonaux :
On peut trouver des égalités de polygonaux à partir
d’un carré magique d’ordre 4. Toutefois, il n’existe pas de règle qui
nous assure qu’une égalité de polygonaux puisse être tirée des rangées.
Égalité de huit polygonaux du même ordre
Examinons les possibilités dans le carré magique
suivant.
En considérant les triangulaires dont l’exposant
est Δ, on peut écrire :
1Δ + 4Δ + 14Δ + 15Δ
= 16Δ + 13Δ + 3Δ + 2Δ = 236
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
En considérant les pentagonaux dont l’exposant est
p, on peut écrire :
11P + 10P + 8P + 5P
= 6P + 7P + 9P + 12P = 448
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
En considérant les hexagonaux dont l’exposant est h,
on peut écrire :
1h + 13h + 8h + 12h = 4h
+ 16h + 5h + 9h = 722
Étudions
un carré magique général dont la somme de chaque rangée horizontale,
verticale et diagonale est 2(2a + 3b + 3c).
Donnons
une valeur à chaque variable. Par exemple, on fait a = 1, b = 2 et c =
5. On obtient le carré magique ci-après dont la somme par rangée est 46.
On peut
établir les propositions suivantes :
• La
somme des polygonaux d’un même ordre de la première ligne est égale à la
somme de ceux de la quatrième ligne.
En considérant les pentagonaux, on
peut écrire :
22p + 3p + 5p
+ 16p = 7p + 18p + 20p + 1p
= 1138
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
• La
somme des polygonaux d’un même ordre de la deuxième ligne est égale à la
somme de ceux de la troisième ligne.
En considérant les hexagonaux dont l’exposant est h,
on peut écrire :
6h + 15h + 13h +
12h = 11h + 10h + 8h + 17h
= 1102
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
• La
somme des polygonaux d’un même ordre de la première colonne est égale à
la somme de ceux de la quatrième colonne.
En considérant les
heptagonaux dont l’exposant est s on peut écrire :
22s + 6s + 11s + 7s
= 16s + 12s + 17s + 1s =
1656
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
• La
somme des polygonaux d’un même ordre de la deuxième colonne est égale à
la somme de ceux de la troisième colonne.
En considérant les
octogonaux dont l’exposant est o on peut écrire :
3o + 15o + 10o +
18o = 5o + 13o + 8o + 20o
= 1882
Cette égalité est vraie pour les polygonaux de tout
ordre y compris pour les carrés.
Égalité de 16 polygonaux du même ordre
Prenons l’égalité qui provient de
la première et de la quatrième ligne du carré magique précédent, soit :
22p + 3p + 5p
+ 16p = 7p + 18p + 20p + 1p
Choisissons un nombre supérieur au
plus grand de l’égalité. Prenons 23. De 23, soustrayons chaque base et
additionnons 23 à chaque base. On peut écrire en ordre numérique :
1p + 7p + 18p
+ 20p + 26p + 28p + 39p + 45p
= 3p + 5p + 16p + 22p + 24p
+ 30p + 41p + 43p = 8578
Cette égalité vaut
pour les polygonaux de tout ordre y compris pour les carrés. Cela est
aussi vrai pour les cubes. 13 + 73 + 183 + 203 + 263 + 283 + 393 + 453 = 33 + 53 + 163 + 223 + 243 + 303 + 413 + 433 = 204 148 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5940
12 mai 2021
Magie 3 × 3 et polygonaux
Un nombre polygonal est un nombre qui peut être représenté par un
polygone régulier constitué de points disposés de façon symétrique.
Voici quatre ordres de polygonaux :
On peut trouver des égalités de polygonaux à partir d’un seul carré
magique et à partir de deux carrés magiques.
Un seul carré magique d’ordre 3
Soit le carré magique suivant dans lequel on considère chaque nombre
comme étant le rang d’un polygonal :
Par exemple, considérons les pentagonaux. Sur la première ligne, on a le
pentagonal de rang 10, le pentagonal de rang 1, le pentagonal de rang 7.
En abrégeant avec l’exposant p qui est mis pour pentagonal, on peut
écrire : 10p = 145, 1p = 1, 7p = 70. La
somme des pentagonaux est 216.
Égalité de six polygonaux du même ordre
Dans tout carré magique 3
×
3, la somme des polygonaux d’un ordre donné est la même dans la première
et la troisième ligne. Il en est ainsi pour la première et la troisième
colonne.
Voici des égalités qui découlent de cette proposition à partir du carré
magique donné :
a) Triangulaires où est Δ est l’exposant
10Δ + 1Δ + 7Δ = 5Δ + 11Δ
+ 2Δ = 84
10Δ + 3Δ + 5Δ = 7Δ + 9Δ
+ 2Δ = 76
b) Carrés où 2 est l’exposant
102 + 12 + 72 = 52 + 112
+ 22 = 150
102 + 32 + 52 = 72 + 92
+ 22 = 134
c) Pentagonaux où p est l’exposant
10P + 1P + 7P = 5P + 11P
+ 2P = 216
10P + 3P + 5P = 7P + 9P
+ 2P = 192
Toutes ces égalités
sont vraies pour les polygonaux de tout ordre.
Égalité de 12 polygonaux du même ordre
Considérons le même carré magique d’ordre 3. Écrivons sous forme
d’égalité les nombres de la première et de la troisième ligne.
10 + 1 + 7 = 5 + 11 + 2 = 18
On prend un nombre qui est supérieur au plus grand nombre de cette
égalité, ordinairement le suivant. On l’appelle l’opérateur. Dans ce
cas-ci, on peut choisir 12. De l’opérateur, on soustrait chacun des
nombres de l’égalité, puis on leur additionne l’opérateur. On obtient :
2 + 22 + 11 + 13 + 5 + 19 = 7 + 17 + 1 + 23 + 10 + 14 = 72
En considérant les heptagonaux dont l’exposant est s et tout en
respectant l’ordre numérique, on peut écrire :
2s + 5s + 11s + 13s + 19s
+ 22s = 1s + 7s + 10s + 14s
+ 17s + 23s = 2802
Cette égalité est vraie pour les polygonaux de tout ordre. Cela
s’applique aussi aux cubes.
23 + 53 + 113 + 133 + 193
+ 223 = 13 + 73 + 103 + 143
+ 173 + 233 = 21 168
Égalité de 24 polygonaux du même ordre
En suivant les mêmes règles et en partant de l’égalité précédente, on
peut trouver une égalité de 24 termes. Comme 23 est la plus grande base,
on choisit 24 comme opérateur.
En considérant les hexagonaux dont l’exposant est h
et en respectant l’ordre numérique,
on peut écrire :
2h + 5h + 11h + 13h + 19h
+ 22h + 26h + 29h + 35h + 37h
+ 43h + 46h = 1h + 7h + 10h
+ 14h + 17h + 23h + 25h + 31h
+ 34h + 38h + 41h + 47h =
18 192
Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi
vrai pour les cubes.
23 + 53 + 113 + 133 + 193
+ 223 + 263 + 293 + 353 + 373
+ 433 + 463 = 13 + 73 + 103
+ 143 + 173 + 233 + 253 + 313
+ 343 + 383 + 413 + 473 =
333 504
Deux carrés magiques d’ordre 3
Prenons maintenant deux carrés magiques qui n’ont aucun lien entre eux.
Égalité de 12 polygonaux du même ordre
La proposition précédente permet de réunir les éléments de certaines
rangées :
• Ligne 1 du carré 1 + ligne 1 du carré 2 = ligne 3 du carré 1 + ligne 3
du carré 2
• Ligne 1 du carré 1 + ligne 3 du carré 2 = ligne 3 du carré 1 + ligne 1
du carré 2
• Colonne 1 du carré 1 + colonne 1 du carré 2 = colonne 3 du carré 1 +
colonne 3 du carré 2
• Colonne 1 du carré 1 + colonne 3 du carré 2 = colonne 3 du carré 1 +
colonne 1 du carré 2
En considérant les triangulaires et en respectant l’ordre numérique, on
peut écrire par rapport aux lignes 1 et 3 :
1Δ
+ 7Δ
+ 10Δ
+ 13Δ
+ 16Δ
+ 22Δ
= 2Δ
+ 5Δ
+ 11Δ
+ 12Δ
+ 18Δ
+ 21Δ
= 564
Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi
vrai pour les cubes.
13
+ 73
+ 103
+ 133
+ 163
+ 223
= 23
+ 53
+ 113
+ 123
+ 183
+ 213
= 18 285
Pour obtenir des égalités comprenant un plus grand nombre de termes, on peut utiliser autant de carrés magiques que l’on veut. Toutefois, s’il y a des doublons de part et d’autre de l’égalité, on les biffe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
5905
21 avril 2021
Récréations mathématiques en classe
Dans le forum du site l’île
des mathématiques, en août 2011, un enseignant dont le pseudonyme
est jamo a fait une critique de Récréomath. Il conclut en écrivant :
« Bon par contre, c'est toujours pareil : c'est bien sympathique d'avoir
des exercices ouverts et ludiques à présenter aux élèves, mais en
pratique il faut reconnaître que ce n'est pas toujours facile à mettre
en application, les élèves prenant ce genre d'activités pas très au
sérieux et c'est un peu le bordel à gérer ... ».
Cet enseignant a raison. L’exploitation de jeux ou récréations
mathématiques à l’école est un art subtil dont la maîtrise est difficile
et qui peut se briser sur de nombreux écueils. C’est pourquoi, j’ai
pensé proposer quelques pistes pour aider les enseignants à utiliser les
mathématiques récréatives à l’école.
Avant de plonger dans une telle aventure, en tant qu’enseignant ou
enseignante, il faut faire un retour sur soi-même et se demander
pourquoi et comment on va procéder.
Si on n’a pas de motif pour introduire des problèmes récréatifs en
classe, vaut mieux oublier cela. En d’autres mots, si on n’a pas
d’objectifs clairs et précis, la situation risque d’être un cauchemar.
Il faut donc se convaincre soi-même de l’intérêt de la démarche. Il faut
être capable d’y voir des bénéfices pour les élèves et, au besoin, de
les noter avant même de commencer. Si l’enseignant n’y croit pas, cela
déteindra dans la présentation qu’il en fera aux élèves. Ces derniers se
demanderont pourquoi ce soudain changement dans l’évolution de la classe
et seront déstabilisés ne sachant pas très bien à quoi cela sert.
Prenons comme exemple un enseignant de mathématiques de 10 ans
d’expériences au secondaire. Il a l’habitude de livrer les notions aux
élèves - d’ailleurs, il le fait bien - et de leur donner des problèmes
visant à assimiler ces notions. Les élèves sont en sécurité.
L’enseignant sait où il va et les élèves sont imprégnés de cette
sécurité.
Un bon jour, 10 minutes avant la fin du cours, cet enseignant dit à
ses élèves : « Dans le programme de mathématiques, il est écrit qu’on
doit vous habituer à la résolution de problèmes. J’en ai préparé un pour
vous. Le voici. »
Relisez attentivement comment l’enseignant s’est exprimé. Il impute
la responsabilité au programme de mathématiques. Donc, il ne s’implique
pas personnellement dans cette démarche. Croit-il vraiment aux bénéfices
de la résolution de problèmes ? A-t-il réfléchi à son déroulement ? Que
signifie pour lui « résolution de problèmes » ? S’est-il demandé ce que
signifiait pour ses élèves cette expression ? A-t-il pensé à la réaction
de ses élèves ?
Comment vont réagir les élèves ? Les uns vont considérer ce temps
comme une récréation ; les autres vont se dire qu’on résout des
problèmes à tous les cours. Ils ne verront pas très bien la pertinence
de cet exercice.
Deux minutes avant la fin du cours, il donnera la solution au
problème, comme il est habitué de le faire. Si certains élèves insistent
pour savoir comment ils auraient dû procéder, il se sent insécure et ne
sait pas par où commencer. Résultat. L’enseignant est heureux quand la
cloche sonne, mais il est malheureux de la tournure des événements.
Pourtant, il sait que, d’habitude quand les élèves sortent de classe,
ils ont progressé et pourraient même quantifier ce progrès. Là, aucun
point de repère. L’exercice a plu à certains élèves et en a ennuyé
d’autres. Qu’ont-ils appris ?
Ajoutons à cela que la tâche de l’enseignant est déjà très exigeante s’il veut que les élèves atteignent les objectifs des programmes d’enseignement et que peu d’enseignants ont reçu une formation qui leur permettent d’être à l’aise dans l’introduction des récréations mathématiques en classe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5875
3 avril 2021
Médaillons à problèmes
Problème.
Roméo a un certain nombre de médaillons. À l’ainé de ses enfants, il en
donne la moitié. Au deuxième, il donne la moitié de ce qui lui reste. Au
troisième, il donne encore la moitié de ce qui lui reste. Il possède
alors 20 médaillons. Combien Roméo avait-il de médaillons ?
Démarche 1
À la fin, il reste 20 médaillons.
On fait : 20 × 2 = 40.
Il reste 40 médaillons. On fait :
40 × 2 = 80.
Il reste 80 médaillons, On fait :
80 × 2 = 160.
Roméo avait 160 médaillons.
Démarche 2
Au
troisième, Roméo donne 20 médaillons. Il avait donc 40 médaillons.
Au
deuxième, Roméo donne 40 médaillons. Il avait donc 80 médaillons.
Au
troisième, Roméo donne 80 médaillons.
Il
a donné 140 médaillons, soit 20 + 40 + 80. À la fin, il lui en reste 20.
On fait : 140 + 20 = 160.
Roméo avait 160 médaillons.
Démarche 3
Procédons par induction. Cette
démarche serait essentielle si le nombre de personnes était très grand.
Soit n le nombre de médaillons qui restent à Roméo. Examinons les cas où n varie de 1 à 3 en procédant à rebours.
• n = 1
À la fin, Roméo possède 1 médaillon. Au troisième, il donne 1 médaillon.
Au deuxième, 2 médaillons. Au premier, 4 médaillons. Il avait 8
médaillons.
• n = 2
À la fin, Roméo possède 2 médaillons. Au troisième, il donne 2
médaillons. Au deuxième, 4 médaillons. Au premier, 8 médaillons. Il
avait 16 médaillons.
• n = 3
À la fin, Roméo possède 3 médaillons. Au troisième, il donne 3
médaillons. Au deuxième, 6 médaillons. Au premier, 12 médaillons. Il
avait 24 médaillons.
Généralisation
Voici deux démarches lorsqu’il reste n médaillons :
Démarche 1. À la fin, Roméo possède n médaillons. Au troisième, il donne
n médaillons. Au deuxième 2n médaillons. Au premier 4n médaillons. Il
avait 8n médaillons.
Par exemple, si n = 20 on fait : 20 × 8 = 160. Si Roméo possède 20
médaillons à la fin, c’est qu’il en avait 160.
Démarche 2. Quand il reste 1 médaillon à Roméo, il en avait 8 : 1 × 8 =
8.
Quand il reste 2 médaillons à Roméo, il en avait 16 : 2 × 8 = 16.
Quand il reste 3 médaillons à Roméo, il en avait 24 : 3 × 8 = 24.
Comme il reste 20 médaillons, on fait : 20 × 8 = 160. Roméo avait
160 médaillons.
Bref, lorsque n prend différentes valeurs, la réponse est 8n. Par
exemple, si on disait qu’il reste 100 médaillons à Roméo, c’est qu’il en
avait 800.
Trois problèmes à résoudre
(solutions à la fin)
1.
Reine donne chaque jour la moitié de ses médaillons plus 1
successivement à ses trois enfants. Il lui reste alors 4 médaillons.
Combien Reine avait-elle de médaillons ?
2.
Roméo a un certain nombre de dés. À l’ainé de ses enfants, il donne le
tiers de ses dés plus 1. Au deuxième, il donne le tiers des dés qui lui
restent plus 1. Au troisième, il donne les 9 dés qui restent. Combien
Roméo avait-il de dés ?
3. Élodie dépense chaque jour la moitié de ce qu’elle possédait plus 1
$. Après quatre jours, elle a tout dépensé. Quelle somme avait-elle ?
………….
Solution 1. Reine avait 46 médaillons.
Solution 2. Roméo avait 24 dés. Solution 3. Élodie avait 30 $. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
5845
15 mars 2021
Expériences en résolution de problèmes
Il
y a 20 ans, j’ai mis en ligne un site de mathématiques récréatives
Récréomath. De temps à autre, je reçois des messages dans lesquels
des enseignants de mathématiques me font part d’expériences qu’ils ont
menées en résolution de problèmes. Voici six témoignages :
1.
Table d’addition
« J’enseigne en sixième au primaire. J’ai dit aux élèves qu’ils allaient
construire une table d’addition. Je les ai invités à préparer une grille
10 × 10, puis d’écrire les nombres de 1 à 9 en abscisse et les mêmes
nombres en ordonnée, puis de faire les additions. Quand cela a été fait,
je leur ai demandé de trouver des régularités dans la table. Quelques
élèves ont trouvé tout de suite des régularités. Je leur ai demandé de
trouver d’autres régularités et leur ai dit qu’on en ferait au cours
suivant. »
2.
Poignées de mains
« J’ai énoncé verbalement à mes élèves le problème suivant :
Cinq enfants se rencontrent. Ils donnent chacun à chacun une poignée de
mains. Combien de poignées de mains seront données. Je leur ai donné
trois minutes pour s’approprier le problème.
Ensuite, j’ai dit aux élèves qu’on ferait une représentation visuelle de
la résolution du problème. Je leur ai dit de bien remarquer ce qui se
passait, parce que je leur demanderais de décrire sur papier ce qu’ils
ont vu. J’ai alors invité cinq élèves à venir former une rangée devant
la classe. Je leur ai dit de donner à chacun une poignée. Comme cette
représentation se faisait dans le désordre, je leur ai demandé de
procéder de façon mieux organisée en leur donnant certains conseils.
Après cela, les élèves ont décrit le procédé utilisé par écrit. J’ai
demandé à un élève de venir expliquer ce procédé. J’ai alors proposé aux
élèves de résoudre le même problème avec 10 enfants. Un élève s’est
exclamé : Cela donnera le double de poignées de mains. Je leur ai
demandé s’ils étaient d’accord avec cela et leur ai dit de proposer une
solution. »
3.
Cartes de problèmes
« J’ai préparé des cartes de problèmes adaptés à mes élèves. À un moment
donné pendant la semaine, je place les élèves en équipes de trois ou de
quatre. Je remets à chaque équipe le même problème. Après un certain
temps, une équipe est invitée à venir expliquer aux autres leur
compréhension du problème, où ils en sont rendus et ce qu’ils ont
découvert. Par la suite, les élèves continuent à résoudre le problème.
Si le temps manque, la tâche se poursuit au cours suivant. »
4.
Problème du jour
« Je suis actuellement enseignant en CE2 et je mets en place dans ma
classe « le problème du jour ». Je donne un problème à un élève la
veille. Il cherche la solution à la maison (avec ou sans aide) et le
lendemain, après vérification de la réponse, il présente lui-même le
problème à ses camarades qui, à leur tour, essaient de le résoudre. On
liste ensuite nos points de réussite, nos difficultés et nos stratégies.
Le
but de cette activité est d’entraîner quotidiennement les élèves à
résoudre des problèmes et à entretenir les stratégies mises en place. »
5.
La valeur de
p
« J’ai demandé aux élèves d’estimer la valeur de
p. Je leur ai
proposé de tracer un grand cercle avec un compas, puis de mesurer le
diamètre. Je leur ai dit de prendre une corde et de mesurer la
circonférence. Je leur ai dit de diviser le résultat obtenu pour la
circonférence par le diamètre et de venir inscrire le quotient au
tableau avec quatre décimales. Je leur ai rappelé la valeur de
p. Chacun a alors calculé sa marge
d’erreur.
Dans un groupe, l’un des élèves a alors dit que pour mesurer la
circonférence, il avait tracé deux diamètres perpendiculaires et qu’il
avait d’abord mesuré le quart de la circonférence pour multiplier
ensuite par 4. Dans un autre groupe, je leur ai demandé de choisir cinq
résultats au hasard et de prendre la moyenne. »
6.
Angles d’un triangle
« Je leur enseignais que la somme des angles intérieurs d’un triangle
est de 180 degrés. J’ai demandé aux élèves de vérifier la mesure de
chaque angle avec un rapporteur d’angle et d’en faire la somme. Après
cette première expérience, j’ai demandé aux élèves de tracer un triangle
quelconque et de noircir les angles. Je leur ai dit de découper les
angles et de les placer pour que les trois zones noircies soient
adjacentes. »
Conclusion J’ai envie de conclure en disant : « Il n’y a pas de petits problèmes ; ils sont tous grands. » En effet, le but visé est, avant tout, d’habituer l’élève à résoudre des problèmes. Tant mieux, si de nouvelles connaissances sont associées à cette démarche. Mais, elles doivent arriver principalement comme des compléments. En effet, avec la technologie contemporaine, il est plus facile d’acquérir des connaissances que des habiletés. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
5815
24 février
2021
Folles dépenses
Problème.
Mélodie dépense chaque jour la moitié de ce qu’elle possédait plus 2 $.
Après quatre jours, elle a tout dépensé.
Quelle somme avait-elle ?
*
* * *
Nous vous présentons six
stratégies.
Stratégie 1. On procède par tâtonnement.
On suppose que Mélodie a 54 $. Le
premier jour, elle dépense d’abord 27 $, puis 2 $, ce qui fait une
dépense de 29 $. Il lui reste : 54 – 29 = 25 $. Ce dernier montant ne
peut pas être impair car on doit diviser par un nombre pair.
On suppose que Mélodie a 56 $. On
fait : (56 – 4)/2 = 26. Il lui reste 26 $. On fait : (26 – 4)/2 = 11. Il
lui reste 11 $. Ce montant ne peut pas être impair.
Cette stratégie peut exiger un
temps considérable. Toutefois, même si elle ne donne pas de résultat
comme c’est le cas ici, elle a l’avantage de nous aider à préciser une
démarche à suivre.
Stratégie 2. On procède par régression.
Une condition connue, c’est le 0 $
de la fin. Procédons du connu à l’inconnu, soit par régression ou à
rebours. On doit transformer les données par des opérations inverses. La
soustraction devient une addition. La division devient une
multiplication. Précédemment, on soustrayait 4 et on divisait par 2.
Dans le cas de la régression, on multiplie par 2 et additionne 4.
Quatrième jour : 0
Troisième jour : 0 × 2 + 4 = 4
Deuxième jour : 4 × 2 + 4 = 12
Premier jour : 12 × 2 + 4 = 28
Auparavant : 28 × 2 + 4 = 60
Mélodie avait 60 $. Elle dépense 32
$ le premier jour. Il lui en reste 28. Elle dépense 16 $ le deuxième
jour. Il lui en reste 12. Elle dépense 8 $ le troisième jour. Il lui en
reste 4. Elle dépense 4 $ le quatrième jour. Il lui en reste 0. Si le
nombre de jours dépassait 4, on n’aurait qu’à appliquer les mêmes
calculs.
Stratégie 3. On généralise.
Dans le premier cas, pour passer de
54 $ à 25 $, on pouvait faire : (54 – 4)/2 = 25. Si on remplace 54 par
n, on peut écrire (n – 4)/2.
On écrit : (n – 4)/2 = 0 qui est le
montant final. D’où n = 4.
On écrit : (n – 4)/2 = 4 qui est le
montant précédent. D’où n = 12.
On écrit : (n – 4)/2 = 12 qui est
le montant précédent. D’où n = 28.
On écrit : (n – 4)/2 = 28 qui est
le montant précédent. D’où n = 60.
Mélodie avait 60 $.
Stratégie 4. On utilise les propriétés des suites.
Le quatrième jour, Mélodie a 0 $.
On fait : 0 × 2 + 4 = 4 comme dans la deuxième stratégie. Le troisième
jour, Mélodie a 4 $. La différence pour les deux jours est 4. On
multiplie successivement par 2. Les différences seront : 8, 16, 32. On
peut écrire : 4 + 8 = 12, 12 + 16 = 28 et 28 + 32 = 60.
Mélodie avait 60 $.
Stratégie 5. On procède par un tableau.
Les montants successifs m sont 0,
4, 12, 28. Les différences successives sont 4, 8, 16, 32. En faisant la
somme, on obtient le total pour chaque jour. Voici le tableau :
Dans le coin inférieur droit, on
trouve 60. Mélodie avait 60 $.
Stratégie 6. On procède de façon algébrique.
Soit x la somme que Mélodie avait.
Le premier jour, il restera (x – 4)/2 à Mélodie. Pour le deuxième jour,
on remplace x par (x – 4)/2 et on simplifie, on obtient (x – 12)/4. Pour
le troisième jour, on remplace le dernier x par (x – 4)/2 et on
simplifie, on obtient (x – 28)/8. Pour le quatrième jour, on remplace
encore le dernier x par (x – 4)/2 et on simplifie, on obtient (x –
60)/16.
On pose : (x – 60)/16 = 0. D’où, x
= 60. Mélodie avait 60 $.
Conclusion
En mathématiques récréatives, ce qui est satisfaisant c’est que
certains problèmes comme celui-ci peuvent être résolus par plus d’une
stratégie. Tentons d’appliquer l’une d’elles sur le problème suivant :
Élodie dépense chaque jour la moitié de ce qu’elle possédait plus 1 $. Après quatre jours, elle a tout dépensé. Quelle somme avait-elle ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
5790
9 février
2021
Un mystère
éclairci
Les mathématiques et en particulier l’arithmétique fourmillent de
situations où, à première vue, on est tenté de parler de mystère.
Démontrer que ces situations ont des fondements mathématiques se fait
par des outils souvent algébriques. En voici un exemple :
Problème 1
•
Choisissez trois chiffres, sauf 0.
•
Formez tous les nombres différents de deux chiffres en utilisant deux
chiffres à la fois.
•
Additionnez ces nombres.
•
Additionnez les chiffres choisis.
•
Divisez l’avant-dernier résultat par le dernier.
Quel est votre résultat ?
Situation 1
•
On choisit 2, 3 et 7.
•
On peut former six nombres : 23, 27, 32, 37, 72, 73.
•
La somme des six nombres est 264.
•
La somme des chiffres est 12.
•
On fait : 264 ÷ 12 = 22
Situation 2
•
On choisit 1, 5 et 8.
•
On peut former six nombres : 15, 18, 51, 58, 81, 85.
•
La somme des six nombres est 308.
•
La somme des chiffres est 14.
•
On fait : 308 ÷ 14 = 22
Le résultat est le même dans les deux situations.
On peut essayer avec d’autres chiffres, le résultat sera toujours le
même, soit 22. Mystère ! L’algèbre peut venir à notre secours.
Situation 3
•
On choisit a, b et c.
•
On peut former six nombres : ab, ac, ba, bc, ca et cb . (Ne pas
confondre avec la multiplication algébrique.)
•
La somme des six nombres pour les unités est 2(a + b + c). Elle est la
même pour les dizaines. Toutefois, pour obtenir la valeur engendrée par
la dizaine, on doit multiplier par 10. On fait : 20(a + b + c) + 2(a + b
+ c) = 22(a + b + c).
•
La somme des chiffres est (a + b + c).
•
On fait : 22(a + b + c) ÷ (a + b + c) = 22.
On
voit que, peu importe les chiffres choisis, le quotient est toujours 22.
Conclusion En généralisant et en faisant les opérations algébriques requises, on a élucidé le mystère. Le choix des chiffres peut changer, le résultat sera toujours le même. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5755
18 janvier 2021
La
bataille des nombres
La bataille des nombres est un jeu
de société, ordinairement à deux joueurs, où il faut atteindre un nombre
en faisant des additions dans une limite donnée. Voici une première
forme de ce jeu :
1. Limite supérieure : 50
Le premier joueur choisit un
nombre de 1 à 5. À tour de rôle, chaque joueur choisit un nombre dans le
même intervalle et l’additionne au dernier nombre énoncé. Le joueur qui
atteint 50 est le gagnant. Le jeu peut se dérouler ainsi :
Joueur A. Il choisit 4.
Joueur B. Il choisit 2 et
l’additionne : ce qui fait 6.
Joueur A. Il additionne 5 : ce qui
fait 11.
Joueur B. Il additionne 3 : ce qui
fait 14.
etc.
À
partir du moment où un joueur connaît le truc, le jeu n’a plus aucun
intérêt. Aussi, il est bon d’introduire des variantes.
2. Variante avec des jetons
On applique
les mêmes règles sauf que chaque joueur a 10 jetons : 2 jetons par
nombre de 1 à 5. Le joueur qui atteint le premier 50 ou plus est le
gagnant.
Dans ce cas,
il est difficile d’appliquer le truc car les jetons qui permettent
d’atteindre un nombre de la suite peuvent manquer.
Si on n’a pas
de jetons, chaque joueur écrit les nombres de 1 à 5 deux fois sur un
bout de papier et les biffe à mesure qu’il les utilise.
3. Variante à rebours
Au lieu de
commencer à 1, on choisit 50 comme nombre de départ. À tour de rôle,
chaque joueur soustrait le nombre qu’il a choisi dans l’intervalle de 1
à 5. Le joueur qui atteint 1 le premier est le gagnant.
La stratégie
gagnante consiste à atteindre
successivement aussitôt que possible les nombres de la suite
arithmétique : 49, 43, 37, 31, 25, 19, 13, 7.
4.
Modifier la limite supérieure
Au
lieu de toujours prendre 50 comme limite supérieure, on peut choisir,
par exemple, un nombre de 40 à 60.
Comment choisir cette limite ?
On
peut inventer sa propre technique. Voici trois suggestions :
1.
Demander à une troisième personne de faire le choix.
2.
Placer dans un sac des jetons comportant les nombres de 40 à 60 et tirer
un jeton au hasard.
3.
Partir de 40. Lancer deux ou trois fois un dé. Additionner.
5. Modifier les intervalles
En
1612, Claude Gaspar Bachet a fixé les bornes de 1 à 100 et l'intervalle
de choix de 1 à 10. Dans ce cas, un joueur peut toujours gagner en
atteignant successivement aussitôt que possible les nombres de la suite
arithmétique : 1, 12, 23, 34, 45, 56, 67, 78 et 89.
On
peut choisir ces règles et adapter les variantes expliquées
antérieurement.
6.
Jouer à qui perd gagne.
Normalement, le joueur qui atteint la limite supérieure gagne. On peut
décider que le
perdant
est
celui qui atteint la limite supérieure ou la dépasse.
7.
Plus de deux joueurs
On
peut s’adonner à ce jeu à plus de deux joueurs. Dans ce cas, on peut
fixer un intervalle différent et une limite supérieure autre.
Conclusion Ce jeu peut être excellent pour développer le calcul mental en rapport avec l’addition et la soustraction, sans compter le plaisir de faire des mathématiques. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5705
18 décembre 2020
Un problème d’âge
ancien
Les frères des écoles chrétiennes (FEC)
ont contribué d’une façon importante à l’éducation des jeunes québécois.
Ils ont enseigné, mais aussi rédigé et édité des manuels scolaires.
« Pendant la première
moitié du 20e siècle, la communauté occupe un des tout
premiers rangs dans l'édition des manuels. Ainsi, durant la décennie
1920, sur les 250 nouveaux manuels publiés au Québec, 37 (14,8 %)
sortent de ses presses ; et la ventilation par titre, permettant
d'isoler les meilleurs vendeurs, illustre encore mieux la prépondérance
des frères des écoles chrétiennes durant la même période : sur les 45
parutions en arithmétique (éditions princeps et réimpressions
confondues), 29 (64,4 %) sont leur fait. » (Les manuels scolaires
québécois, Université Laval, 2012)
Un des manuels scolaires
des FEC est Arithmétique, Cours complémentaire. Dans l’édition de
1926, à la page 351, on peut lire ce problème que nous allons étudier.
« Le carré de l’âge de Simon égale
16 fois l’âge qu’il aura dans 12 ans. Quel est son âge actuel ? »
Ce problème se trouve dans la
section des équations du second degré. Par le fait même, l’élève est
invité à résoudre ce problème en appliquant la mécanique des équations
de ce degré : ce qui est bien, mais ce qui, par ailleurs, ne se situe
pas dans la résolution de problèmes où l’élève doit choisir ses
stratégies.
1.
Compréhension du problème
Il arrive souvent que les élèves
sont incapables de traduire un énoncé en des phrases mathématiques. Dans
ce cas, les enseignant(e)s de mathématiques sont portés à dire que les
élèves ne savent pas lire.
Un truc efficace pour bien
comprendre le problème est de faire une hypothèse. Dans ce cas-ci,
supposons que l’âge de Simon est 20, on pourra écrire :
202 = 16(20 + 12). On a donc : 400 = 512, ce qui
est faux, mais utile pour écrire une équation.
2. Résolution
algébrique
Dans l’égalité précédente, 20 est
le nombre hypothétique cherché. On le remplace par x. On peut écrire : x2 = 16(x + 12). L’équation transformée est x2
– 16x – 192 = 0. En décomposant en facteurs, on obtient : (x + 8)(x –
24) = 0. D’où, x' = -8 et x'' = 24. Comme il n’existe pas d’âge négatif,
on rejette – 8. Simon a 24 ans.
3. Propriétés des nombres
Si on n’a pas de connaissances algébriques, on
peut résoudre ce problème en appliquant les propriétés des nombres.
C’est un domaine malheureusement boudé dans l’enseignement des
mathématiques.
3.1 Multiples de 4
Comme un des facteurs de l’égalité est 16, le
nombre cherché est un multiple de 4. On essaie 4, 8, 12, 16, etc. comme
étant le nombre cherché. Par exemple, si on prend 4, on peut écrire 42
= 16(4 + 12), ce qui correspond à 16 = 256. La valeur 4 ne convient pas.
On continue jusqu’à 24. Simon a 24 ans.
3.2 Facteur de 16
Comme le nombre de gauche est un carré et que
16 est aussi un carré, il faut que le facteur de 16 soit un carré. On
essaie 4, 13, 24. Par exemple, si on prend 13, on peut écrire 132
= 16(13 + 12), ce qui correspond à 169 = 400. La valeur 13 ne convient
pas. On vérifie avec 24. Simon a 24 ans.
3.3
Égalité de carrés
Cette stratégie est similaire à la
précédente, mais le raisonnement pour y arriver est différent.
L’équation est :
x2 = 16(x + 12). On extrait la
racine carrée de part et d’autre. On obtient x = ±4√(x + 12). Pour avoir
un carré sous le radical, il faut donner à x les valeurs 4, 13, 24.
Simon a 24 ans.
Conclusion
En tablant sur les propriétés des
nombres, on peut éviter des calculs qui peuvent s’avérer difficiles. Par
exemple, ce n’est pas tout le monde qui peut décomposer
x2 – 16x – 192 = 0 en facteurs.
Bref, ce problème d’allure simple peut nécessiter jusqu’à quatre stratégies. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5675
30 novembre 2020 La Dame de pique
Problème 1
Chaque soir avant de se
coucher, Léa joue à la dame de pique sur son portable. Elle joue
toujours deux parties et, quand elle a terminé, elle consulte les
statistiques de ses gains. Lorsqu’elle gagne les deux parties, son taux
de gain augmente. Lorsqu’elle perd les deux parties, son taux de gain
diminue. Qu’en est-il de son taux de gain lorsqu’elle gagne une partie
et qu’elle perd l’autre ?
Démarche
Tout d’abord, disons que le
nombre de parties gagnées augmente d’une unité lorsque le gain suit la
perte ou dans le sens inverse. Supposons que Léa a gagné auparavant 45
parties sur 100, en perdant d’abord, elle est créditée de 45 parties sur
101. Comme elle gagne la fois suivante, elle atteint 46 parties sur 102.
Dans la même hypothèse, en gagnant d’abord, elle atteint 46 parties sur
101. Comme elle perd la fois suivante, elle est à 46 parties sur 102. Le
résultat final est le même dans les deux cas.
Trois cas peuvent se
présenter.
1. Le taux est inférieur à 50
%.
Supposons que 45 parties sur
100 ont été gagnées auparavant. Le taux de départ est de 45 %. Après
deux parties, Léa a gagné 46
parties sur 102 : ce qui correspond à 45,098 %. Le taux de gain a donc
augmenté de 0,098 %, soit près d’un dixième d’un pourcent.
2. Le taux est égal à 50 %.
Supposons que 50 parties sur
100 ont été gagnées auparavant. Le taux de départ est de 50 %. Après
deux parties, Léa a gagné 51 parties sur 102 : ce qui correspond à 50 %.
Dans ce cas, le taux de gain ne change pas.
3. Le taux est supérieur à 50
%.
Supposons que 70 parties sur
100 ont été gagnées auparavant. Le taux de départ est de 70 %. Après
deux parties, Léa a gagné 71 parties sur 102 : ce qui correspond à 69,6
%. Dans ce cas, le taux de gain a diminué de 0,4 %.
En guise de conclusion
Bref, quand on joue deux
parties de conclusions différentes, peu importe dans quel sens la perte
ou le gain survient, il y a un léger gain au-dessous de 50 %, pas de
changement à 50 % et une légère perte au-dessus de 50 %. C’est une loi
mathématique cruelle pour les joueurs qui sont heureux de dépasser les
50 % de gain.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5640
9 novembre 2020
Un nouveau
livre
Je
viens de publier aux Éditions Goélette un nouveau livre récréatif. Son
titre est Défis logiques. Sur
le
même modèle,
il contient 115 problèmes
qui consistent à reconstituer logiquement des ensembles d'éléments ayant
des relations entre eux. Voici un exemple :
Trois pères ont construit chacun une cabane à oiseaux en des années
différentes. Sur chaque cabane, ils ont écrit le nom de leur enfant.
Pères : Alfredo, Claudio, Fernando
Enfants : Bertin, Horace, Magalie
Années : 2017, 2018, 2020
1. Le nom de Magalie n’apparaît pas sur la cabane construite en 2018.
2. La cabane marquée Horace a été construite après celle de Claudio.
3. Fernando a construit sa cabane avant la pandémie de 2020 et n’y a pas
écrit Horace.
4. Alfredo a écrit le nom de son garçon sur sa cabane construite après
2017.
5. Claudio n’a pas construit sa cabane en 2017.
Pour chaque père, découvrez le nom de l’enfant et l’année de construction de la cabane. » |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5625
30 octobre 2020
Polygonaux et carrés magiques
Soit le carré
magique d’ordre 3 suivant :
Considérons
chaque nombre comme étant le rang d’un nombre triangulaire. Par exemple,
on a 11Δ = 66 (11Δ se lit triangulaire de rang 11,
onzième triangulaire ou 11 triangulaire), 2Δ = 3, 8 Δ
= 36, etc. On obtient :
Ce carré
n’est pas magique. Toutefois, la somme des triangulaires de la première
ligne est 105 comme celle de la troisième ligne. Aussi, la somme des
triangulaires de la première colonne est 97 comme celle de la troisième
colonne.
Ces égalités
de sommes sont-elles toujours vraies ? Commençons par produire un carré
magique général.
La somme dans
chaque ligne, colonne et diagonale est 0.
Proposition 1. Si on convertit chaque terme en un nombre
triangulaire, la somme des nouveaux termes est la même dans la première
et la troisième ligne.
Justification. On écrit : x Δ + (-x – y) Δ + y
Δ = -yΔ + (x + y)Δ - xΔ. On
développe les nombres triangulaires sur le modèle (n2 + n)/2
lorsque n est le rang. On a :
(x2
+ x)/2 + [(x2 + 2xy + y2) + (-x – y)]/2 + (y2
+ y)/2 = (-y2 – y)/2 + [(x2 + 2xy + y2)
+ (x + y)]/2 + (x2 – x)/2
Après
simplification, chaque membre de l’égalité est égal à (x2 +
xy + y2). La somme est donc la même dans la première ligne et
dans la troisième ligne.
Proposition 2. Si on convertit chaque terme en nombre
triangulaire, la somme des nouveaux termes est la même dans la première
et la troisième colonne.
Justification. On peut procéder de la même façon que précédemment ou
encore s’appuyer sur le fait qu’un carré magique demeure magique quand
on fait sa rotation.
Proposition 3. Les deux premières propositions sont vraies
pour les triangulaires et pour tous les autres nombres polygonaux, soit
les carrés, les pentagonaux, les hexagonaux, les heptagonaux, etc.
À partir du
carré magique suivant, on peut écrire les égalités ci-après :
a)
Triangulaires
14Δ
+ 2Δ + 11Δ = 7Δ + 16Δ + 4Δ
= 174
14Δ
+ 6Δ + 7Δ = 11Δ + 12Δ + 4Δ
= 154
b) Carrés
142
+ 22 + 112 = 72 + 162 + 42
= 321
142
+ 62 + 72 = 112 + 122 + 42
= 281
c)
Pentagonaux où p est l’exposant. Par exemple, 14p est le
quatorzième pentagonal.
14p
+ 2p + 11p = 7p + 16p + 4p
= 468
14p
+ 6p + 7p = 11p + 12p + 4p
= 408
d) Hexagonaux
où p est l’exposant. Par exemple, 14h est le quatorzième
hexagonal.
14h + 2h + 11h = 7h + 16h
+ 4h = 615
14h + 6h + 7h = 11h + 12h
+ 4h = 535
e)
Heptagonaux où s est l’exposant. Par exemple, 14s est le
quatorzième heptagonal.
14s + 2s + 11s = 7s + 16s
+ 4s = 762
14s + 6s + 7s = 11s + 12s
+ 4s = 662
e) Octogonaux
où o est l’exposant. Par exemple, 14o est le quatorzième
octogonal.
14o + 2o + 11o = 7o + 16o
+ 4o = 909
14o + 6o + 7o = 11o + 12o
+ 4o = 789
On note que
la différence entre les deux sommes d’un même nombre polygonal est
successivement 20, 40, 60, 80, 100 et 120.
Conclusion Ces découvertes permettent d’approfondir davantage les polygonaux et, espérons-le, d’y trouver ultérieurement d’autres propriétés intéressantes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5600
15 octobre 2020
Des
neveux et nièces
Problème 1. Dorothée, Françoise et Gaétane sont trois sœurs. Dorothée a 3
neveux. Françoise a 6 neveux. Gaétane a 5 neveux.
Combien
chacune a-t-elle de fils ?
Solution 1. Soit d le nombre de fils de Dorothée, f celui de Françoise, g
celui de Gaétane. On écrit :
f + g = 3
d + g = 6
d + f = 5
On additionne
les trois équations. On obtient : 2d + 2f + 2g = 14. En simplifiant, on
a : d + f + g = 7. Puisque f + g = 3, alors d = 4. Puisque d + g = 6,
alors f = 1. Puisque d + f = 5, alors g = 2.
Dorothée a 4
fils. Françoise a 1 fils. Gaétane a 2 fils.
Solution 2. On peut aussi procéder ainsi :
• On
additionne les nombres de neveux.
• On divise
par 2.
• Du
résultat, on soustrait chaque nombre de neveux.
On fait : 3 +
6 + 5 = 14, 14 ÷ 2 = 7, 7 – 3 = 4 (Dorothée), 7 – 6 = 1 (Françoise) et 7
– 5 = 2 (Gaétane).
Dorothée a 4
fils. Françoise a 1 fils. Gaétane a 2 fils.
Problème 2. Marcel, Normand, Pierre et Quentin sont quatre frères. Marcel a 8
nièces. Normand a 7 nièces. Pierre a 9 nièces. Quentin a 6 nièces.
Combien
chacun a-t-il de filles ?
Solution 1. Soit m le nombre de filles de Marcel, n celui de Normand, p celui
de Pierre et q celui de Quentin. On écrit :
n + p + q = 8
m + p + q = 7
m + n + q = 9
m + n + p = 6
On additionne
les quatre équations. On obtient : 3m + 3n + 3p + 3q = 30. En
simplifiant, on a : m + n + p + q = 10. Puisque n + p + q = 8, alors m =
2. Puisque m + p + q = 7, alors n = 3. Puisque m + n + q = 9, alors p =
1. Puisque m + n + p = 6, alors q = 4.
Marcel a 2
filles. Normand a 3 filles. Pierre a 1 fille. Quentin a 4 filles.
Solution 2. On peut aussi procéder ainsi :
• On
additionne les nombres de nièces.
• On divise
par 3.
• Du
résultat, on soustrait chaque nombre de nièces.
On fait : 8 +
7 + 9 + 6 = 30, 30 ÷ 3 = 10, 10 – 8 = 2 (Marcel), 10 – 7 = 3 (Normand),
10 – 9 = 1 (Pierre), 10 – 6 = 4 (Quentin).
Marcel a 2
filles. Normand a 3 filles. Pierre a 1 fille. Quentin a 4 filles.
Complément Dans ce dernier cas, pour connaître le nombre de filles, on additionne les nombres de nièces et on divise par 3. Le résultat est 10. On compte 10 filles. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5575
30 septembre 2020
Enjeux de jetons
Problème 1. Xavier et Yvon jouent deux parties avec des jetons et en
perdent chacun une dans cet ordre. Ils conviennent que celui qui perdra
doublera le nombre de jetons de l’autre. À la fin, chacun a 12 jetons.
Combien chacun avait-il de jetons au début ?
Solution 1. Au début, Xavier a x et Yvon a y jetons.
Xavier perd. Il doit donner
y à Yvon. Il reste (x – y) à Xavier et Yvon a 2y.
Yvon perd. Il doit donner (x
– y) à Xavier. Il reste à Yvon (3y – x) et Xavier a (2x – 2y). Ce
tableau illustre la situation :
On peut
écrire : 2x – 2y = 12 et 3y – x = 12. On trouve que x = 15 et y = 9.
Xavier avait 15 jetons et Yvon 9 jetons.
Solution 2.
On procède à
rebours. Les perdants sont inversés. Les gagnants perdent la moitié de
leur avoir.
Xavier avait 15 jetons et Yvon 9 jetons.
Problème 2. Xavier, Yvon et Zénon jouent trois parties et en perdent
chacun une dans cet ordre. Ils conviennent que celui qui perdra doublera
le nombre de jetons de l’autre. À la fin, chacun a 24 jetons.
Combien chacun avait-il de jetons au début ?
Solution.
On procède à
rebours. Les perdants sont inversés. Les gagnants perdent la moitié de
leur avoir.
Xavier avait
39 jetons, Yvon 21 jetons et Zénon 12 jetons.
Problème 3. Xavier, Yvon et Zénon jouent trois parties et en perdent
chacun une dans cet ordre. Ils conviennent que celui qui perdra donnera
à chacun des deux autres la moitié des jetons qu’il a. À la fin, chacun
a 27 jetons.
Combien chacun avait-il de jetons au début ?
Solution.
On procède à
rebours. Les perdants sont inversés. Les gagnants perdent le tiers de
leur avoir.
Xavier avait 35 jetons, Yvon 26 jetons et Zénon 20 jetons. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 5540
9 septembre 2020
Un
rectangle magique troué
Problème.
Placez les nombres de 1 à 12 dans la grille ci-après pour que la somme
soit la même dans chacune des six rangées de trois cases adjacentes.
Solution. Six cases appartiennent à deux rangées : les cases marquées 2.
Elles sont de degré 2. Les six autres appartiennent à seulement une
rangée. Elles sont de degré 1. Voici l’illustration :
La somme des nombres de 1 à 12 est 78. Supposons qu’on dispose les
éléments de 1 à 6 dans les cases de degré 2 et les éléments de 7 à 12
dans les cases de degré 1. On peut alors écrire : 2(1 + 2 + 3 + 4 + 5 +
6) + (7 + 8 + 9 + 10 + 11 + 12) = 99. C’est une somme indexée.
Comme il y a six rangées, on divise 99 par 6. Le quotient est 16,5. En
conséquence, la plus petite somme probable par rangée est 17.
La somme par rangée est 17
Pour que la somme par rangée soit 17, il faut que la somme indexée soit
102. En effet, 17 × 6 = 102. Précédemment, la somme indexée trouvée a
été de 99. Il y a donc une différence de 3. On peut permuter 4 et 7, 5
et 8, 6 et 9 d’un ensemble à l’autre pour obtenir 102.
■
Permutation de 4 et de 7
Les cases de degré 2 devront recevoir 1, 2, 3, 5, 6, 7. Pour les cases
de degré 1, ce sera 4, 8, 9, 10, 11, 12. On peut écrire : 2(1 + 2 + 3 +
5 + 6 + 7) + (4 + 8 + 9 + 10 + 11 + 12) = 102.
Il n’y a pas de triplets dont la somme est 17 dans les éléments de degré
2. Donc, il n’y a pas de configuration dans ce cas.
■
Permutation de 5 et de 8
On peut écrire : (1 + 2 + 3 + 4 + 6 + 8)2
+ (5 + 7 + 9 + 10 + 11 + 12) = 102.
Il y a un seul triplet (3, 6, 8) dans les éléments de degré 2. On
commence par placer ce triplet dans la deuxième colonne. Puis, on
complète en ayant soin de respecter les degrés. On peut obtenir cette
configuration.
■
Permutation de 6 et de 9
On peut écrire : 2(1 + 2 + 3 + 4 + 5 + 9) + (6 + 7 + 8 + 10 + 11 + 12) =
102.
Dans les éléments de degré 2, il y a un seul triplet (3, 5, 9) dont la
somme est 17. Pour configurer la grille, on procède comme précédemment.
On peut obtenir :
Autres sommes possibles
Les autres sommes possibles sont de 18 à 22. Voici une configuration
quand la somme est 22 :
Tentez de trouver d’autres configurations pour les sommes de 17 à 22. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Suite des propos mathématiques | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


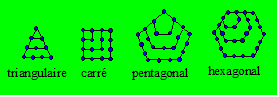
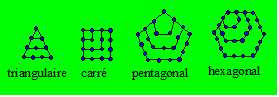
 « 5.
Oiseaux choyés
« 5.
Oiseaux choyés