|
(Dessin réalisé au primaire) Contactez-moi : cejean@charleries.net |
Les charleries Bienvenue sur mon blogue, Ce blogue contient des souvenirs, des anecdotes, des opinions, de la fiction, des bribes d’histoire, des récréations et des documents d’archives. Charles-É. Jean
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Propos mathématiques |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4505
25 octobre 2018
Pyramides d’ordre 3
Une pyramide
numérique est un ensemble de nombres disposés dans les cases d'un
tableau de forme triangulaire de telle manière que chaque nombre d'une
rangée supérieure est égal à la somme des deux nombres inférieurs
adjacents.
À moins de spécifications
contraires, on considère seulement les entiers positifs.
Voici un exemple de pyramide :
Cette pyramide est dite d’ordre 3 car elle contient trois cases à
la base et trois rangées horizontales.
1. Sommet de la pyramide
Proposition 1. Dans une pyramide d’ordre 3, le
sommet S est obtenu en additionnant la somme des termes extrêmes de la
base et le double du terme central.
Soit A, B et C les nombres de la
base dans cet ordre. En complétant la configuration, on trouve que le
sommet est A + 2B + C.
Bref, S = (A + C) + 2B.
Problème. Trouvez le nombre du sommet dans une pyramide d’ordre 3
quand la somme des termes de la base est 20 et quand le terme central
est 4 et ce, sans trouver les nombres des cases intermédiaires.
Solution. La somme des termes extrêmes de la base est 16. On
écrit :
S = (A + C) + 2B = 16 + 2 × 4 = 24. Le sommet est
24. Voici un exemple de configuration :
2. Différence du sommet et de la
base
Proposition 2. Dans une pyramide d’ordre 3, la différence du sommet
S et du total T des termes de la base est égale au terme central de la
base.
On fait : (A + 2B + C) – (A + B + C) = B.
Bref, S – T = B.
Problème. Configurez une pyramide d’ordre 3 lorsque le total des
termes de la base est 15 et le sommet est 22.
Solution. On fait : 22 – 15 = 7. D’où, A + C = 8. Voici un exemple
de configuration :
3. Somme des termes
Proposition 3. Dans une pyramide d’ordre 3, la somme Σ de tous les
termes est obtenue en additionnant 3 fois la somme des termes extrêmes
de la base et cinq fois le terme central.
Soit A, B, C les nombres de la base dans cet ordre. On remplit
toutes les cases. En additionnant tous les termes, on obtient 3A + 5B +
3C.
Bref, Σ = 3(A + C) + 5B.
Problème. Trouvez une configuration où la somme de tous les termes
est 58.
Solution. On pose : 3(A + C) + 5B = 58. C’est une équation du
premier degré à deux inconnues. Il y a trois possibilités.
1) Si A + C = 6, alors B = 8
2) Si A + C = 11, alors B = 5
3) Si A + C = 16, alors B = 2
Voici une configuration à partir de la dernière possibilité :
Problème. Trouvez une configuration où la somme des termes est 69
et dont le sommet est 24.
Solution. On écrit :
Σ = 3(A + C) + 5B = 69
S =
(A + C) + 2B = 24
On résout le système d’équations. On trouve que B = 3 et A + C =
18. Voici une configuration :
4. Variations du sommet
Proposition 4. Soit trois entiers différents à la base. Le sommet
varie selon l’ordre de disposition des termes à la base.
1er cas. Pour avoir le plus petit sommet, on place le
plus petit entier dans la case centrale de la base et les deux autres
dans les extrémités.
2e cas. Pour avoir le plus grand sommet, on place le
plus grand entier dans la case centrale de la base et les deux autres
dans les extrémités.
5. Sommet avec des entiers
consécutifs
Proposition 5. Dans une
pyramide d’ordre 3, lorsque la base contient trois entiers consécutifs
dans l’ordre, le sommet S est égal à quatre fois le terme central de la
base.
À la base, on écrit successivement A, A + 1, A + 2. On remplit
toutes les cases. Au sommet, on trouve 4A + 4.
Bref, S = 4(A + 1).
Voici un exemple de configuration dans lequel A = 5 :
6. Plus petit sommet avec des
entiers consécutifs
Proposition 6. Dans une pyramide d’ordre 3 où A est le plus petit
terme, lorsque la base contient des entiers consécutifs dans le
désordre, le plus petit sommet est 4A + 3.
7. Plus grand sommet avec des
entiers consécutifs
Proposition 7. Dans une pyramide d’ordre 3 où A est le plus petit
terme, lorsque la base contient des entiers consécutifs dans le
désordre, le plus grand sommet est 4A + 5.
Problème. Construisez une pyramide formée de trois entiers
consécutifs dans le désordre à la base et dont le plus grand sommet est
65.
Solution. Soit A le plus petit terme, le plus grand sommet est 4A +
5. On écrit : 4A + 5 = 65. D’où, A = 15 et A + 2 = 17. Une configuration
est :
Voici un tableau qui illustre certaines propositions lorsque la
base contient des entiers consécutifs dans l’ordre ou dans le désordre :
8. Somme des termes avec des
entiers consécutifs
Proposition 8. Dans une pyramide d’ordre 3, lorsque la base
contient des entiers consécutifs dans l’ordre, la somme de tous les
termes est égale à 11 fois le terme du centre.
D’après la proposition 3, Σ = 3(A + C) + 5B. À la base, on a
successivement A, A + 1, A + 2. On peut écrire : Σ = 3(A + A + 2) + 5(A
+ 1) = 11A + 11.
Bref, Σ = 11(A + 1).
Par exemple, on suppose que A = 6. On peut écrire : Σ = 11(A + 1) =
77. Voici une configuration dans laquelle la somme de tous les termes
est 77 :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4520
3 novembre 2018
Pyramides d’ordre 4
Une pyramide numérique est un ensemble de nombres disposés dans les
cases d'un tableau de forme triangulaire, de telle manière que chaque
nombre d'une rangée supérieure est égal à la somme des deux nombres
inférieurs adjacents.
À moins de spécifications contraires, on considère seulement les entiers
positifs.
Voici un exemple de pyramide :
Cette pyramide est dite d’ordre 4 car elle contient quatre cases à la
base et quatre rangées horizontales.
1. Sommet de la pyramide
Proposition 1.
Dans une pyramide d’ordre 4, le sommet S est obtenu en additionnant la
somme des termes extrêmes de la base et le triple de la somme des deux
termes centraux.
Soit A, B, C, D les nombres de la base dans cet ordre. En complétant la
configuration, on trouve que le sommet est A + 3B + 3C + D.
Bref, S = (A + D) + 3(B + C).
Problème. Trouvez le nombre du sommet dans une pyramide d’ordre 4 quand
la somme des termes de la base est 27 et que la somme des deux termes
centraux est 12, sans trouver les nombres des cases intermédiaires.
Solution. La somme des deux termes extrêmes de la base est 15. On
écrit : (A + D) + 3(B + C) = 15 + 3 × 12 = 51. Voici un exemple de
configuration :
Pour avoir toujours le même sommet, il faut que la somme des termes
extrêmes soit 15 et que la somme des deux termes centraux soit 12. Voici
une autre configuration :
2. Différence du sommet et de la base
Proposition 2. Dans une pyramide d’ordre 4, la différence du sommet S et
du total T de la base est égale à deux fois la somme des deux termes
centraux de la base.
On fait : (A
+ 3B + 3C + D)
– (A + B + C + D) = 2B + 2C.
Bref, S – T = 2(B + C).
Problème. Configurez une pyramide d’ordre 4 lorsque la somme des termes
de la base est 15 et que le sommet est 27.
Solution. On applique la formule précédente. On fait : 27 – 15 = 2(B +
C). D’où, B + C = 6. On commence alors par remplir les deux cases
centrales de la base avec une somme de 6. Puis, on complète les deux
autres cases avec une somme de 9. Voici un exemple de configuration :
3. Somme des termes
Proposition 3. Dans une pyramide d’ordre 4, la somme Σ de tous les
termes est obtenue en additionnant 4 fois la somme des deux termes
extrêmes de la base et 9 fois la somme des deux termes centraux.
Soit A, B, C, D les nombres de la base dans cet ordre. On remplit toutes
les cases. En additionnant tous les termes, on obtient 4A + 9B + 9C +
4D.
Bref, Σ = 4(A + D) + 9(B + C).
Problème. Trouvez une configuration où la somme de tous les termes est
101.
Solution. On pose : 4(A + D) + 9(B + C) = 101. C’est une équation du
premier degré à deux inconnues. Il y a deux possibilités.
1) Si A + D = 5, alors B + C = 9
2) Si A + D = 14, alors B + C = 5
Voici une configuration à partir de la deuxième possibilité :
Problème. Trouvez une configuration où la somme des termes est 100 et
dont le sommet est 31.
Solution. On écrit :
4(A + D) + 9(B + C) = 100 (somme des termes)
(A + D) + 3(B + C) = 31 (sommet)
On résout le système d’équations. On trouve que A + D = 7 et que B + C =
8. Voici une configuration :
4. Variations du sommet
Proposition 4. Soit quatre entiers différents à la base. Le sommet varie
selon l’ordre des termes à la base.
1er cas. Pour avoir le plus petit sommet, on place les deux
plus petits entiers dans les deux cases centrales et les deux autres
dans les extrémités.
2e cas. Pour avoir le plus grand sommet, on place les deux
plus grands entiers dans les deux cases centrales et les deux autres
dans les extrémités.
5. Sommet avec des entiers consécutifs
Proposition 5. Dans une
pyramide d’ordre 4, lorsque la base contient quatre entiers consécutifs
dans l’ordre, le sommet S est égal à quatre fois la somme du double du
plus petit entier et de 3.
À la base, on écrit successivement A, A + 1, A + 2, A + 3. On remplit
toutes les cases. Au sommet, on trouve 8A + 12 qui est égal à 4(2A + 3).
Bref, S = 4(2A + 3) où 2A + 3 est la somme des deux termes extrêmes ou
des deux termes centraux.
Voici un exemple de configuration dans lequel A = 4 :
Démonstration. Montrez que, dans une pyramide d’ordre 4, lorsque la base
contient quatre entiers consécutifs dans l’ordre, le sommet S est égal à
deux fois le total T des termes de la base.
6. Plus petit sommet avec des entiers consécutifs
Proposition 6. Dans une pyramide d’ordre 4 où A est le plus petit terme,
lorsque la base contient des entiers consécutifs dans le désordre, le
plus petit sommet est 8(A + 1).
7. Plus grand sommet avec des entiers consécutifs
Proposition 7. Dans une pyramide d’ordre 4 où A est le plus petit terme,
lorsque la base contient des entiers consécutifs dans le désordre, le
plus grand sommet est 8(A + 2).
Problème. Construisez une pyramide formée de quatre entiers consécutifs
dans le désordre à la base dont le plus grand sommet est 72.
Solution. Soit A le plus petit terme, le plus grand sommet est 8(A + 2).
On écrit : 8(A + 2) = 72. D’où, A = 7. Une configuration est :
Voici un tableau qui illustre certaines propositions lorsque la base
contient des entiers consécutifs dans l’ordre ou dans le désordre :
8. Somme des termes avec des entiers consécutifs
Proposition 8. Dans une pyramide d’ordre 4, lorsque la base contient des
entiers consécutifs dans l’ordre, la somme de tous les termes est égale
à 13 fois la somme du double du plus petit entier et de 3.
D’après la proposition 3, Σ = 4(A + D) + 9(B + C). À la base, on a
successivement A, A + 1, A + 2, A + 3. On peut écrire : Σ = 4(A + A + 3)
+ 9(A + 1 + A + 2) = 26A + 39.
Bref, Σ = 13(2A + 3).
Par exemple, on suppose que A = 4. On peut écrire : Σ = 13(2A + 3) =
143. Voici une configuration dans laquelle la somme de tous les termes
est 143 :
Démonstration. Montrez que, lorsque la base contient des entiers consécutifs dans l’ordre, la somme Σ de tous les termes est égale à 6,5 fois le total T des termes de la base. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4545
18 novembre 2018
Pyramides d’ordre 5
Une pyramide numérique est un ensemble de nombres disposés dans les
cases d'un tableau de forme triangulaire de telle manière que chaque
nombre d'une rangée supérieure est égal à la somme des deux nombres
inférieurs adjacents.
À moins de spécifications contraires, on considère seulement les entiers
positifs.
Voici un exemple de pyramide :
Cette pyramide est dite d’ordre 5 car elle contient cinq cases à la base
et cinq rangées horizontales.
1. Sommet de la pyramide
Proposition 1. Dans une pyramide d’ordre 5, le sommet S est obtenu en
additionnant la somme des termes extrêmes de la base, le quadruple de la
somme des deux termes voisins et le sextuple du terme central.
Soit A, B, C, D, E les nombres de la base dans cet ordre. En complétant
la configuration, on obtient comme sommet A + 4B + 6C + 4D + E.
Bref, S = (A + E) + 4(B + D) + 6C.
Problème 1. Quel est le sommet dans cette configuration ?
Solution. On peut écrire :
On voit que 2B + 9 = 15. D’où, B = 3. On procède de la même façon pour
trouver la valeur de D. On écrit : 2D + 13 = 25. D’où, D = 6.
On remplace les lettres par leur valeur dans (A + E) + 4(B + D) + 6C. Le
sommet est 74.
2. Différence du sommet et de la base
Proposition 2.
Dans une pyramide d’ordre 5, la différence du sommet S et du total T de
la base est obtenue en additionnant le triple de la somme des termes
voisins des extrémités et le quintuple du terme central.
On fait : (A + 4B + 6C + 4D + E) – (A + B + C + D + E) = 3B + 5C + 3D.
Bref, S – T = 3(B + D) + 5C.
Problème. Configurez une pyramide d’ordre 5 lorsque la somme des termes
de la base est 22 et le sommet est 67.
Solution. On fait : 67 – 22 = 3(B + D) + 5C. C’est une équation du
premier degré à deux inconnues. Il y a deux possibilités.
1) Si C = 3, B + D = 10.
2) Si C = 6, B + D = 5.
Choisissons la dernière hypothèse. Comme la somme de la base est 22, A +
E = 11. Avec ces données, on peut établir la configuration suivante.
3. Somme des termes
Proposition 3. Dans une pyramide d’ordre 5, la somme Σ de tous les
termes est obtenue en additionnant 5 fois la somme des termes extrêmes
de la base, 14 fois la somme des termes voisins des extrêmes et 19 fois
le terme du milieu.
Soit A, B, C, D, E les nombres de la base dans cet ordre. On remplit
toutes les cases. En additionnant tous les termes, on obtient Σ = 5A +
14B + 19C + 14D + 5E.
Bref,
Σ
= 5(A + E) + 14(B + D) + 19C.
Problème. Trouvez une configuration dans laquelle la somme des termes
est 271, A + E = 10 et B + D = 9.
Solution. Dans l’équation 5(A + E) + 14(B + D) + 19C = 271, on remplace
(A + E) et (B + D) par leur valeur. On obtient : C = 5. Il existe
plusieurs configurations. Pour en trouver une, il s’agit de donner des
valeurs aux lettres dont les sommes sont données. La somme des termes
sera toujours 271. Voici un exemple de configuration :
4. Variations du sommet
Proposition 4. Soit cinq entiers différents à la base. Le sommet varie
selon l’ordre de disposition des termes à la base.
1er cas. Pour avoir le plus petit sommet, on place le plus
petit entier dans la case centrale, les deux entiers suivants dans les
cases adjacentes et les deux derniers entiers dans les extrémités.
2e cas. Pour avoir le plus grand sommet, on place le plus
grand entier dans la case centrale, les deux entiers suivants dans les
cases adjacentes et les deux derniers entiers dans les extrémités.
5. Sommet avec des entiers consécutifs
Proposition 5. Dans une pyramide d’ordre 5, lorsque la base contient des
entiers consécutifs dans l’ordre, le sommet S est égal à 16 fois la
somme du plus petit terme et de 2.
À la base, on écrit successivement A, A + 1, A + 2, A + 3, A + 4. On
remplit toutes les cases. Au sommet, on trouve 16A + 32.
Bref, S = 16(A + 2).
6. Plus petit sommet avec des entiers consécutifs
Proposition 6. Dans une pyramide d’ordre 5 où A est le plus petit terme,
lorsque la base contient des entiers consécutifs dans le désordre, le
plus petit sommet est (16A + 19).
7. Plus grand sommet avec des entiers consécutifs
Proposition 7. Dans une pyramide d’ordre 5 où A est le plus petit terme,
lorsque la base contient des entiers consécutifs dans le désordre, le
plus grand sommet est (16A + 45).
Le tableau suivant illustre les dernières propositions.
Problème. Trouvez une configuration dans laquelle on place à la base
cinq entiers consécutifs, mais pas nécessairement dans l’ordre et dans
laquelle le sommet est 95.
Solution. En se basant sur la proposition 6, on fait : 16A + 19 = 95.
D’où, A = 4,75. Si A = 4, le plus petit sommet est 83 et le plus grand
est 109. Les termes de la base sont 4, 5, 6, 7 et 8. D’où, la somme des
termes de la base est 30. On écrit :
A + 4B + 6C + 4D + E = 95
A + B + C + D + E = 30
En soustrayant les deux équations, on obtient 3B + 5C + 3D = 65, soit
3(B + D) + 5C = 65.
La plus petite valeur possible de C est 4. Si C = 4, alors B + D = 15.
On place 4 au centre. La combinaison de deux nombres dont la somme est
15 est (7, 8). On place 7 et 8 autour du centre, puis on complète avec 5
et 6 dans les extrémités. On peut obtenir le tableau suivant.
8. Somme des termes avec des entiers consécutifs
Proposition 8. Dans une pyramide d’ordre 5, lorsque la base contient des
entiers consécutifs dans l’ordre, la somme de tous les termes est égale
à 57 fois la somme du plus petit entier et de 2.
D’après la proposition 3,
Σ
= 5(A + E) + 14(B + D) + 19C. À la base, on a successivement A, A + 1, A
+ 2, A + 3, A + 4. On peut écrire : Σ = 5(A + A + 4) + 14(A + 1 + A + 3)
+ 19(A + 2) = 57A + 114.
Bref, Σ = 57(A + 2). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4565
30 novembre 2018
Pyramides d’ordre 6
Une pyramide
numérique est un ensemble de nombres disposés dans les cases d'un
tableau de forme triangulaire, de telle manière que chaque nombre d'une
rangée supérieure est égal à la somme des deux nombres inférieurs
adjacents.
À moins de spécifications
contraires, on considère seulement les entiers positifs.
Voici un exemple de pyramide :
Cette pyramide est dite d’ordre 6 car elle contient six cases à la
base et six rangées horizontales.
1. Sommet de la pyramide
Proposition 1. Dans une pyramide d’ordre 6, le sommet S est obtenu
en additionnant la somme des termes extrêmes de la base, cinq fois la
somme des deux termes voisins des extrémités et 10 fois la somme des
deux termes centraux.
Soit A, B, C, D, E, F les nombres de la base dans cet ordre. En
complétant la configuration, on trouve que le sommet est A + 5B + 10C +
10D + 5E + F.
Bref, S = (A + F) + 5(B + E) + 10(C + D).
Appliquons cette formule, pour vérifier le sommet dans la figure
précédente. On a : (2 + 7) + 5(5 + 3) + 10(4 + 1) = 9 + 40 + 50 = 99. Le
sommet est bien 99.
Problème. Dans cette configuration, trouvez le sommet sans faire
tous les calculs intermédiaires.
Solution. On commence par trouver les entiers manquants de la base.
On recherche la valeur de B en construisant ce tableau.
Comme 2B + 9 = 21, alors B = 6. En procédant de la même façon, on
trouve que D = 1.
Le sommet est (A + F) + 5(B + E) + 10(C + D). On applique cette
formule : (7 + 9) + 5(6 + 4) + 10(2 + 1) = 16 + 50 + 30 = 96. Voici la
configuration :
2. Différence du sommet et de la
base
Proposition 2. Dans une pyramide d’ordre 6, la différence du sommet
S et du total T de la base est obtenue en additionnant quatre fois la
somme des termes voisins des extrémités de la base et neuf fois la somme
des termes centraux.
On fait (A + 5B + 10C + 10D + 5E + F) – (A + B + C + D + E) = 4B +
9C + 9D + 4E.
Bref, S – T = 4(B + E) + 9(C + D).
3. Somme des termes
Proposition 3. Dans une pyramide d’ordre 6, la somme Σ de tous les
termes est obtenue en additionnant 6 fois la somme des termes extrêmes
de la base, 20 fois la somme des termes voisins des extrêmes et 34 fois
la somme des deux termes du milieu.
Soit A, B, C, D, E, F les nombres de la base dans cet ordre. On
remplit toutes les cases. En additionnant tous les termes, on obtient 6A
+ 20B + 34C + 34D + 20E + 6F.
Bref, Σ = 6(A + F) + 20(B + E) + 34(C + D).
Problème. Sans faire toutes les additions au long, trouvez la somme
de tous les termes de la pyramide du point 1.
Solution. On fait : 6(7 + 9) + 20(6 + 4) + 34(2 + 1) = 96 + 200 +
102 = 398.
Problème. Complétez la configuration suivante pour que la somme de
tous les termes soit 348.
Solution. Dans l’équation : 6(A + F) + 20(B + E) + 34(C + D) = 348,
on remplace (B + E) et (C + D) par leur valeur. On obtient : A + F = 13.
Il existe plusieurs configurations. Pour en trouver une, il s’agit de
donner des valeurs arbitraires à A et à F où A + F = 13. La somme des
termes sera toujours 348. Voici un exemple de configuration :
4. Variations du sommet
Proposition 4. Soit six entiers différents à la base. Le sommet
varie selon l’ordre de disposition des termes à la base.
1er cas. Pour avoir le plus petit sommet, on place les
deux plus petits entiers dans les deux cases centrales, les deux entiers
suivants dans les cases adjacentes et les deux derniers entiers dans les
extrémités.
2e cas. Pour avoir le plus grand sommet, on place les
deux plus grands entiers dans les deux cases centrales, les deux entiers
suivants dans les cases adjacentes et les deux derniers entiers dans les
extrémités.
5. Sommet avec des entiers
consécutifs
Proposition 5. Dans une pyramide d’ordre 6, lorsque la base
contient six entiers consécutifs dans l’ordre, le sommet S est égal à 16
fois la somme du double du plus petit et de 5.
À la base, on écrit dans l’ordre A, A + 1, A + 2, A + 3, A + 4, A +
5. On remplit toutes les cases. Au sommet, on trouve 32A + 60.
Bref, S = 16(2A + 5). Par exemple, si A = 3, alors S = 176.
6. Plus petit sommet avec des
entiers consécutifs
Proposition 6. Dans une pyramide d’ordre 6 où A est le plus petit
terme, lorsque la base contient des entiers consécutifs dans le
désordre, le plus petit sommet est 4(8A + 11).
7. Plus grand sommet avec des
entiers consécutifs
Proposition 7. Dans une pyramide d’ordre 6 où A est le plus petit
terme, lorsque la base contient des entiers consécutifs dans le
désordre, le plus grand sommet est 4(8A + 29).
8. Somme des termes avec des
entiers consécutifs
Proposition 8. Dans une pyramide d’ordre 6, lorsque la base
contient des entiers consécutifs dans l’ordre, la somme de tous les
termes est égale à 16 fois la somme du double du plus petit et de 5.
D’après la proposition 3,
Σ = 6(A + F) + 20(B + E) + 34(C +
D). À la base, on a successivement A, A + 1, A + 2, A + 3, A + 4, A + 5.
On peut écrire : Σ = 6(A + A + 5) + 20(A + 1 + A + 4) + 34(A + 2 + A +
3) = 120A + 300.
Bref, Σ = 60(2A + 5). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4480
10 octobre 2018
Un
triangle magique
Sur les côtés
de ce triangle, on doit placer les nombres de 1 à 9 dans les cases
jaunes pour que la somme soit identique sur chacun des côtés.
Les sommes
possibles des côtés varient de 17 à 23. En effet, la somme des nombres
de 1 à 9 est 45. Les nombres sur chacun des sommets doivent être comptés
deux fois pour établir la somme. Les plus petits éléments aux sommets
sont possiblement 1, 2 et 3, soit une somme de 6. On fait : 45 + 6 = 51
et 51 ÷ 3 = 17. La plus petite somme possible sur les côtés est 17.
Les plus
grands éléments aux sommets sont possiblement 7, 8 et 9, soit une somme
de 24. On fait : 45 + 24 = 69 et 69 ÷ 3 = 23. La plus grande somme
possible sur les côtés est 23.
Faisons
l’étude de quelques cas afin de trouver des solutions.
1. Une somme de 17
On place 1, 2
et 3 dans les sommets. Les couples (1, 3), (3, 2) et (2, 1) se
retrouvent respectivement chacun sur un côté. Le manque sur chaque
côté est de 13, 12 et 14. Cela correspond aux paires (6, 7), (4, 8) et
(5, 9). On remplit la figure avec ces données.
Une deuxième
solution peut être trouvée.
2. Une somme de 18
La somme des
sommets devra être 9. Il y a trois possibilités pour les sommets : (1,
2, 6), (1, 3, 5), (2, 3, 4).
a) La
possibilité est (1, 2, 6)
Il manque sur
les côtés 15, 10 et 11. Les nombres qui restent sont : 3, 4, 5, 7, 8, 9. On
ne peut pas former tous les couples. Il n’y a pas de solution dans ce
cas.
b) La
possibilité est (1, 3, 5)
Il manque sur
les côtés 14, 10 et 12. Les nombres qui restent sont : 2, 4, 6, 7, 8, 9. On
ne peut pas former tous les couples. Il n’y a pas de solution dans ce
cas.
c) La
possibilité est (2, 3, 4)
Il manque sur
les côtés 13, 11 et 12. Les nombres qui restent sont : 1, 5, 6, 7, 8, 9. On
ne peut pas former tous les couples. Il n’y a pas de solution dans ce
cas.
3. Une somme de 19
La somme des
sommets doit être 12. Il y a sept possibilités pour les sommets : (1, 2,
9), (1, 3, 8), (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6) et (3, 4, 5).
Il y a deux solutions lorsque les sommets sont 1, 4 et 7.
Nous vous
laissons le soin de trouver d’autres solutions.
4. Une somme de 20
Nous vous
donnons une solution quand les sommets sont 3, 5 et 7.
5. Une somme de 21
La somme des
sommets doit être 18. On a le même nombre de solutions que pour la somme
19. Pour les trouver, de 10, on soustrait chacun des éléments. On
appelle cela une figure complémentaire. Voici le triangle complémentaire
de la première solution de la somme 19 :
6. Une somme de 22
La somme des
sommets doit être 21. Comme il n’y a pas de solution pour la somme 18,
il n’y en a pas pour la somme 22.
7. Une somme de 23
La somme sur
les sommets doit être 24. On a le même nombre de solutions que pour la
somme 17. Pour les trouver, de 10, on soustrait chacun des éléments.
Voici le triangle complémentaire de la première solution de la somme
17 :
Vous pouvez trouver d’autres solutions.
Problème 1. On décide de placer les nombres impairs de 1 à 17.
Combien y a-t-il de sommes possibles ?
Problème 2. On décide de placer les nombres de la suite 1, 4, 7, 10, 13, 16, 19, 22, 25. Trouvez au moins une configuration. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4450
22 septembre 2018
Des
carrés à profusion
Dans cet
article, nous allons indiquer un procédé pour trouver des identités de
carrés à partir d’un tableau.
On commence
par établir la somme de deux carrés dont la somme des bases est un
nombre donné. Par exemple, on choisit 21 comme somme des bases.
On recherche
une identité dans laquelle les sommes du tableau apparaissent. Par
exemple, on peut écrire : 401 + 245 = 365 + 281 = 646.
On remplace
chaque nombre par sa valeur puisée dans le tableau, soit la somme de
deux carrés :
12
+ 202 + 72 + 142 = 22 + 192
+ 52 + 162 = 646
On remet les
termes de l’identité en ordre :
12
+ 72 + 142 + 202 = 22 + 52
+ 162 + 192 (A)
Les identités
continuent d’exister dans les cas suivants.
• Lorsqu’on
biffe l’exposant dans l’identité A. On a :
1 + 7 + 14 +
20 = 2 + 5 + 16 + 19 = 42
• Lorsque
l’exposant est 3 au lieu de 2 dans l’identité A. On a :
13
+ 73 + 143 + 203 = 23 + 53
+ 163 + 193 = 11 088 (B)
• Lorsqu’on
additionne un nombre à chaque terme de l’identité A. Voici un exemple où
on additionne 1 :
22
+ 82 + 152 + 212 = 32 + 62
+ 172 + 202 = 734
• Lorsqu’on
additionne un nombre à chaque terme de l’identité B. Voici un exemple où
on additionne 2 :
33
+ 93 + 163 + 223 = 43 + 73
+ 183 + 213 = 15 500
On peut aussi
trouver des identités avec les nombres polygonaux (triangulaire,
pentagonal, hexagonal, heptagonal, etc.). Soit ∆ l’exposant d’un nombre
triangulaire tel que 9∆ = 45. On peut lire : le triangulaire
de 9 est 45. Voici un exemple avec les triangulaires où dans l’identité
A on remplace l’exposant 2 par l’exposant ∆ :
1∆
+ 7∆ + 14∆ + 20∆ = 2∆ + 5∆
+ 16∆ + 19∆
1 + 28 + 105
+ 210 = 3 + 15 + 136 + 190 = 344
Voici un exemple avec les
pentagonaux où on admet que l’exposant est p :
1p
+ 7p + 14p + 20p = 2p + 5p
+ 16p + 19p
1 + 70 + 287
+ 590 = 5 + 35 + 376 + 532 = 948
Problème. Dans le tableau suivant, la somme des bases est 18 :
a) Trouvez
une identité comportant six nombres dont les trois nombres du premier
membre sont 180, 194 et 290.
b) Trouvez
une identité de sommes de carrés à partir de ces nombres.
c) Vérifiez
si l’identité demeure vraie quand on élève les termes au cube.
Bref, le
procédé peut produire un nombre incalculable d’identités. En même temps,
il est relativement facile à appliquer.
……………………….
Solutions.
a) On peut
écrire : 290 + 194 + 180 = 260 + 234 + 170 = 664
b) 12
+ 172 + 52 + 132 + 62 + 122
= 22 + 162 + 32 + 152 + 72
+ 112 = 664
L’identité en
ordre est :
12
+ 52 + 62 + 122 + 132 + 172
= 22 + 32 + 72 + 112 + 152+
162 = 664
c) L’identité
demeure vraie quand on élève au cube.
13
+ 53 + 63 + 123 + 133 + 173
= 23 + 33 + 73 + 113 + 153+
163 = 9180 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4430
10 septembre 2018
Élucubrations sur huit chiffres
Nous allons étudier six situations où on compose quatre
nombres de deux chiffres avec les chiffres de 1 à 8 pris chacun une
seule fois.
Problème 1. Trouvez la plus petite somme.
Solution. On écrit les plus petits chiffres dans la colonne des
dizaines et les autres dans celle des unités. L’ordre dans lequel les
chiffres sont placés dans une colonne n’a pas d’importance.
On a : 15 + 26 + 37 + 48 = 126. La plus petite somme est 126.
Problème 2. Trouvez la plus grande somme.
Solution. On intervertit les chiffres de chaque colonne du tableau
précédent. On a : 51 + 62 + 73 + 84 = 270. La plus grande somme est 270.
Problème 3. Tous les nombres entre 126 et
270 peuvent-ils être des sommes ?
Solution. Non. La somme des chiffres de 1 à 8 est 36, un multiple
de 9. Or, dans une addition, si la somme des chiffres est un multiple de
9, le résultat est un multiple de 9. En conséquence, des sommes comme
127, 128, 129, 130, 131, 132, 133, 134 ne sont pas possibles. La somme
qui suit 126 est 135. Voici un exemple de disposition des chiffres :
Cela donne : 18 + 36 + 24 + 57 = 135.
Problème 4. Combien y a-t-il de sommes
possibles ?
Solution. Les sommes appartiennent à la suite 126, 135, 144, …,
261, 270. Pour trouver le nombre de sommes, on procède ainsi :
• On établit la différence entre la plus grande et la plus petite
somme.
• On divise par 9.
• On additionne 1.
On fait : (270 – 126)/9 + 1 = 17. Il y a 17 sommes possibles.
Problème 5. Comment trouver la nouvelle
somme si on remplace un chiffre d’une colonne par un chiffre d’une autre
colonne sans faire à nouveau la somme des quatre nombres ?
Solution. Intervertissons le 1 et le 4 du tableau précédent. La
dizaine passe de 1 à 4. Il y a augmentation de 30. L’unité passe de 4 à
1. Il y a diminution de 3. Cela fait, au total, une augmentation de 27.
Sachant que la somme du tableau est 135, on fait : 135 + 27 = 162. La
nouvelle somme est 162. Si le déplacement de chiffres amène une
diminution, on soustrait au lieu d’additionner.
Pour calculer l’augmentation ou la diminution, on peut procéder
autrement.
• On soustrait les deux chiffres déplacés.
• On multiplie par 9.
Dans le cas où l’unité passe de 4 à 1, on fait : 4 – 1 = 3 et 3 × 9
= 27.
Autre astuce. On peut tout simplement former deux nombres avec les
chiffres donnés et soustraire ces deux nombres. On fait : 41 – 14 = 27.
Problème 6. Trouvez quatre nombres de deux
chiffres (1 à 8) dont la somme est 225.
Solution. On commence par les unités.
• La somme des unités ne peut pas être 5, car la plus petite somme
de quatre chiffres est 10 : 1 + 2 + 3 + 4.
• La somme des unités peut être 15. Dans ce cas, la somme des
dizaines est 21, car la somme de tous les chiffres est 36. La somme des
quatre nombres est alors 225, car 210 + 15 = 225. On pourra avoir comme
solution : 31 + 52 + 64 + 78.
• La somme des unités peut être 25. Dans ce cas, la somme des
dizaines est 11, car la somme de tous les chiffres est 36. La somme des
quatre nombres est alors 135, car 110 + 25 = 135. La somme n’est pas
225.
• La somme des unités ne peut pas être 35, car la plus grande somme
de quatre chiffres est 26 : 5 + 6 + 7 + 8.
Appliquez vos connaissances en résolvant les quatre problèmes
suivants.
Problème 7. Trouvez quatre nombres de deux
chiffres (1 à 8) dont la somme est 171.
Problème 8. Trouvez quatre nombres de deux
chiffres (1 à 8) dont la somme est 207
Problème 9. Trouvez deux nombres de quatre
chiffres (1 à 8) dont la somme est 6543.
Problème 10. Trouvez trois nombres de deux
chiffres (1 à 6) dont la somme est 102. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4410
19 juin 2018
Calendrier découpé
À première vue, on ne voit pas de lien entre le calendrier et les
carrés. Pourtant, il est possible de trouver des égalités de sommes de
carrés à partir du calendrier.
Commençons par délimiter une grille carrée 3 × 3 comme ci-après
dans une feuille de calendrier.
1. On peut obtenir une égalité respectivement de sommes de trois
carrés en prenant, dans la grille ci-après, les nombres dont les cases
sont bleues d’une part et rouges d’autre part. On élève au carré chacun
de ces nombres.
On peut écrire : 32 + 122 + 182 =
42 + 102 + 192 = 477. On constate que
seuls les nombres de la diagonale de droite ne sont pas utilisés. De
plus, 3 + 12 + 18 = 4 + 10 + 19 = 33.
2. Voici un autre cas :
On peut écrire : 42 + 122 + 172 =
52 + 102 + 182 = 449. On constate que
seuls les nombres de la diagonale de gauche ne sont pas utilisés. De
plus, 4 + 12 + 17 = 5 + 10 + 18 = 33.
3. On peut obtenir une égalité respectivement de sommes de quatre
carrés illustrés selon les couleurs. Les nombres soulignés apparaissent
deux fois dans le même membre de l’égalité :
On peut écrire : 32 + 52 + 112 +
112 = 42 + 42 + 102 + 122
= 276. On constate que seuls les nombres de la troisième ligne ne sont
pas utilisés. De plus, 3 + 5 + 11 + 11 = 4 + 4 + 10 + 12 = 30.
4. Voici un autre cas où les nombres soulignés apparaissent deux
fois dans le même membre de l’égalité :
On peut écrire : 32 + 52 + 182 +
182 = 42 + 42 + 172 + 192
= 682. On constate que seuls les nombres de la deuxième ligne ne sont
pas utilisés. De plus, 3 + 5 + 18 + 18 = 4 + 4 + 17 + 19 = 44.
5. Voici un autre cas :
On peut écrire : 102 + 122 + 182 +
182 = 112 + 112 + 172 + 192
= 892. On constate que seuls les nombres de la première ligne ne sont
pas utilisés. De plus, 10 + 12 + 18 + 18 = 11 + 11 + 17 + 19 = 58.
6. Voici un autre cas :
On peut écrire : 32 + 112 + 112 +
172 = 42 + 102 + 102 + 182
= 540. On constate que seuls les nombres de la troisième colonne ne sont
pas utilisés. De plus, 3 + 11 + 11 + 17 = 4 + 10 + 10 + 18 = 42.
7. Il existe d’autres cas. Sauriez-vous en trouver ?
Conclusion. Ce que nous avons affirmé est vrai pour toute grille
carrée 3 × 3
du calendrier. C’est aussi vrai pour toute autre grille 3 × 3
qui contient des nombres ayant la même différence dans chaque
ligne, puis dans chaque colonne. Cette différence peut être la même ou
pas des lignes aux colonnes. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
4390
7 juin 2018
Jeux de chiffres
Le chiffre 9 est riche en situations surprenantes. Par exemple, les
multiples consécutifs de 9 inférieurs à 9 sont 18, 27, 36, 45, 54, 63,
72, 81, 90. Dans la colonne des dizaines, on peut lire consécutivement
les chiffres de 1 à 9. Dans la colonne des unités, on peut lire ces
mêmes chiffres en ordre décroissant. De plus, la somme des chiffres de
chaque multiple est 9.
Arrêtons-nous à étudier des nombres de trois chiffres qui
contiennent chacun des chiffres de 1 à 9.
Problème 1. Trouvez la plus petite somme de
trois nombres de trois chiffres qui contiennent chacun des chiffres de 1
à 9.
Solution 1. On écrit les chiffres consécutifs de 1 à 9 ainsi :
On a : 147 + 258 + 369 = 774. La plus petite somme est 774. Dans
chaque colonne, on peut changer les chiffres de place sans changer la
somme. Par exemple, on pourrait avoir : 248 + 359 + 167 = 774.
Problème 2. Trouvez la plus grande somme.
Solution 2. On écrit les chiffres consécutifs de 1 à 9 ainsi :
On a : 741 + 852 + 963 = 2556. La plus grande somme est 2556. Comme
dans le cas précédent, dans chaque colonne, on peut changer les chiffres
de place sans changer la somme.
Problème 3. Les sommes 774 et 2556 sont
divisibles par 9. Montrez que toute autre somme est divisible par 9.
Solution 3. La somme des chiffres de 1 à 9 est 45. Or, 45 est
divisible par 9. Donc, toute somme est divisible par 9.
Problème 4. Soit trois nombres : 147 + 258 +
369 dont la somme est 774. Dans les mêmes conditions, trouvez trois
nombres dont la somme est immédiatement supérieure à 774.
Solution 4. D’après la proposition précédente, la prochaine somme
devrait être 783. En effet, après 774, le prochain nombre divisible par
9 est 783.
Pour y arriver, dans les trois nombres de départ, on choisit des
chiffres consécutifs étant l’un dans la colonne des dizaines et l’autre
dans la colonne des unités. On permute ces deux chiffres. Les deux
chiffres consécutifs sont 6 et 7. On les permute. On a donc : 146 + 258
+ 379 = 783.
En fait, dans la colonne des dizaines on a ajouté une dizaine, soit
10, et, dans la colonne des unités, on a retranché 1. Or, 10 – 1 = 9 :
ce qui est la différence entre les deux sommes.
Problème 5. Comment trouver un trio de nombres
dont la somme est, par exemple, 2052 ?
(Dans le problème 1, la somme des centaines est 6, la somme des
dizaines est 15, la somme des unités est 24. On a : 6 + 15 + 24 = 45.
C’est comme si on avait : 600 + 150 + 24 = 774. Par ailleurs, la somme
minimale dans chaque colonne est 6 et la somme maximale est 24.)
Revenons au problème. La somme des unités pourra être 12 ou 22.
Choisissons 12. La somme des dizaines pourra être 14 ou 24. Choisissons
14. On fait : 45 – 12 – 14 = 19. D’où, la somme des centaines est 19. En
distribuant les chiffres, on peut obtenir : 231 + 854 + 967 = 2052.
Problème 6. À votre tour, dans les mêmes conditions, trouvez trois nombres dont la somme est 999. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4295
15 avril 2018
Un problème de cartes
Problème 1
©
©
©
§
§
§
§
ª
ª
ª
ª
ª
©
©
©
©
©
©
§
§
§
§
§
§
§
Combien y aura-t-il de symboles dans la 100e
ligne ?
Démarche
La première ligne contient 3 symboles, la deuxième ligne 4 symboles, la
troisième ligne 5 symboles. La différence entre le nombre de symboles et
le rang de la ligne est 2.
La 100e ligne contiendra 102 symboles.
Problème 2
Quels seront les symboles dans la 100e ligne ?
Démarche
Chaque symbole apparaît à toutes les trois lignes. On fait : 100
¸ 3 =
33 reste 1. Le reste correspond à la première ligne où on observe des
symboles de cœur.
On aura les symboles de
cœur dans la 100e ligne.
Problème 3
En tout, combien aura-t-on écrit de symboles de trèfle si la 100e
ligne est la dernière ?
Démarche
On construit un tableau qui donne le nombre de trèfles selon le rang de
chaque ligne visée.
Les trèfles apparaissent sur la deuxième ligne, la cinquième, la
huitième, etc. La dernière ligne qui contient du trèfle est la 98e
de la figure, car 98 ÷ 3 = 32 reste 2. Elle contient 100 trèfles. Il
s’agit d’additionner les nombres de la suite
4, 7, 10, 13, 16, …, 94, 97, 100.
On calcule le nombre de couples dont la somme est 104 (4 + 100, 7 +
97, 10 + 94,
etc.). Pour cela, on fait : 100 ÷ 3 = 33 reste 1. On conserve le
quotient. On compte 33 couples. La moyenne de chaque couple est 52. On
fait : 33
× 52 = 1716.
On aura écrit 1716 symboles de trèfle.
Problème 4
(à résoudre)
Dans quelle ligne atteindra-t-on le 100e cœur ? (Dans la 22e
ligne) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4225
13 mars 2018
Jeu
de Berloquin
Texte de Jean-Marc Gervais qui
fait suite à l’article #4075
Je vous écris à propos du jeu de Pierre Berloquin. Il fallait compléter un carré de 5 sur 5 avec les nombres entiers de 6 à 25 de telle façon que la somme soit égale à 65 sur chaque ligne, chaque colonne et chaque diagonale.
Voici le carré à compléter :
Voici la solution proposée par
l'auteur de ce jeu :
Je vous avais fait remarquer que,
dans les colonnes 3 et 5, il y avait 2 sommes égales : 11 + 15 = 26 et 9
+ 17 = 26 et que l'on pouvait ainsi trouver une autre solution.
Dans
Charleries/Propos Mathématiques, vous faites remarquer que, si on
additionne les nombres de la deuxième ligne avec les nombres
correspondants de la quatrième ligne, on obtient toujours la somme 26.
À partir de cette remarque, on
peut déjà trouver 6 solutions au problème (la solution proposée plus
cinq autres).
J'ai aussi remarqué qu'il y a deux
sommes égales dans la première et la cinquième ligne : 3 + 25 = 28 et 24
+ 4 = 28.
On peut donc permuter le 3 de la
première ligne avec le 24 de la cinquième, et aussi le 25 de la première
avec le 4 de la cinquième.
Comme 6 × 2 = 12, on peut donc
trouver 12 solutions (au moins). Les voici :
Y a-t-il d’autres solutions ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4200
3 mars 2018
Truc pour poser des équations
Il arrive que
certains élèves aient peu de succès en algèbre. Quand arrive le temps de
résoudre des problèmes qui doivent être traduits en équations, ils sont
perdus. Ils ne savent pas comment s’y prendre.
Je vous donne
un truc qui permet de poser des équations. Il s’agit de supposer une
réponse possible et par la suite de traduire le tout en une équation en
remplaçant la réponse hypothétique par x.
Problème 1.
Érika et Fernande ont le même avoir. Érika dépense 30 $ et Fernande
75 $. Alors, le montant d’argent qui reste à Érika est le double de
celui de Fernande.
Combien chacune avait-elle ?
Démarche. On
suppose que chacune avait 100 $. On peut écrire :
100 – 30 = 70
(Érika)
100 – 75 = 25
(Fernande)
On devrait
avoir : (100 – 75) × 2 = (100 – 30).
Soit x
l’avoir de chacune. On remplace 100 par x dans la dernière égalité. On
aura :
(x – 75) × 2
= x – 30.
Une fois
l’équation résolue, on trouve que x = 120. Chacune avait 120 $.
Problème 2.
Une somme de 76 $ est composée de pièces de 2 $ et de pièces de 5
$. Le nombre de pièces de monnaie est 20.
Combien y en a-t-il de chaque espèce ?
Démarche. On
suppose qu’il y a 9 pièces de 2 $. On peut écrire :
9 × 2 = 18
(20 – 9) × 5
= 55
On devrait
avoir : 9 × 2 + (20 – 9) × 5 = 76.
Soit x le
nombre de pièces de 2 $. On remplace 9 par x. On aura :
x × 2 + (20 –
x) × 5 = 76
Une fois l’équation résolue, on
trouve que x = 8. Il y a 8 pièces de 2 $ et 12 pièces de 5 $. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4165
17 février 2018
Suites arithmétiques de degré 2
Une suite arithmétique de degré 1 est une suite de nombres dont chaque
terme diffère du précédent d’une quantité fixe appelée raison.
Ainsi, l’ensemble des nombres entiers consécutifs forme une suite
arithmétique de degré 1 dont la raison est 1. Par ailleurs, 2, 5, 8, 11,
14, … est aussi une suite arithmétique de degré 1 mais dont la raison
est 3. Le terme général d’une telle suite est an + b où n est le rang du
terme.
La raison d’une suite arithmétique de degré supérieur à l’unité n’est
pas une constante, mais les termes successifs d’une suite du degré
inférieur. Pour construire une suite arithmétique de degré 2, il faut un
premier terme et une suite arithmétique de degré 1. Par exemple, en
partant avec 4 et en utilisant la suite 2, 5, 8, 11, 14, ...
comme raison, on obtient la suite de degré 2 suivante : 4, 6, 11,
19, 30, 44, ...
Le terme général d’une suite arithmétique de degré 2 est an2
+ bn + c où n est le rang du terme. Pour trouver ce terme, il faut
notamment connaître les trois premiers termes. Nous vous donnons une
façon de trouver le ne terme d’une telle suite.
Soit les trois premiers termes 5, 7, 13. On écrit :
a + b + c = 5
4a + 2b + c = 7
9a + 3b + c = 13
En soustrayant la première équation de la deuxième, on obtient : 3a + b
= 2. En soustrayant la deuxième équation de la troisième, on obtient :
5a + b = 6. En soustrayant ces deux dernières équations, on obtient : 2a
= 4. D’où, a = 2. On remplace a par 2 dans une des dernières équations.
On obtient : b = –4. On remplace a et b par leur valeur respective dans
l’équation du début. On obtient : c = 7. Le terme général est 2n2
– 4n + 7.
On peut vérifier si le terme général est exact.
Si n = 1, on a : 2 – 4 + 7 = 5.
Si n = 2, on a : 8 – 8 + 7 = 7.
Si n = 3, on a : 18 – 12 + 7 = 13.
Ces trois résultats sont bien les trois premiers termes de la suite.
Pour connaître le 10e terme, on remplace n par 10 dans le
terme général. Cela donne : 200 – 40 + 7 = 167. Le 10e terme
est 167.
Pour trouver les valeurs de a, b et c, on peut appliquer une technique :
a = [(3e terme – 2e terme) – (2e terme
– 1er terme)]/2
b = (2e terme – 1er terme) – 3a
c = (1e terme) – a – b
La raison de la suite 5, 7, 13, … est 2, 6, 10, 14, 18, … soit une suite
arithmétique de degré 1 dont la raison est 4. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4140
7 février 2018
Coûts au début du 20e siècle
Au cours des ans, les problèmes
arithmétiques nous en apprennent sur le coût des produits et des
services de l’époque. Nous avons étudié certains problèmes donnés à des
examens de fin d’année au début du 20e siècle pour découvrir
ces quelques renseignements donnés ici en vrac.
Les données numériques sont à
prendre avec circonspection. On ne sait jamais si c’est le plus bas ou
le plus haut prix. Nonobstant cette remarque, cela donne un ordre de
grandeur.
En 1900
1. Une chemise coûte 1,35 $ avec 19 cents de profit pour le
commerçant.
2. Un ouvrier gagne 75 cents par jour. Comme il travaille 10 heures
par jour, il gagne 7 ½ cents
de l’heure. S’il travaille 6 jours par semaine, comme c’est le cas à
l’époque, il gagne annuellement 234 $. Dans d’autres problèmes à la même
époque, on mentionne 80 cents et même 1 $ comme salaire journalier.
3. La dépense courante d’une personne adulte seule est de 38 cts
par jour, soit 138,70 $ par année.
4. Une maison se vend 2400 $ et une autre, 2700 $.
5. Un billet est escompté à la banque à 7 ½ %.
En 1901
6. La vitesse d’un bateau à vapeur est de 12 milles à l’heure. Dans
ce cas, pour parcourir la distance de Rimouski à Montréal, il fallait
autour de 26 heures.
7. Une livre de café se vend 35 cents. Une livre de thé se vend 65
cents.
8. Une montre coûte 55 $. Le bijoutier l’a payée 45 $.
9. Une once d’or vaut 20,67 $. En 1970, elle valait 35 $.
Aujourd’hui, elle vaut plus de 1000 $.
En 1902
10. Un homme dépense 12 $ par mois pour sa nourriture, 5 $ par mois
pour son logement, 4 $ par mois pour son habillement. Si on traduit cela
par an, on a 144 $ pour sa nourriture, 60 $ pour son logement, 48 $ pour
son habillement.
11. La population de l’Europe est de 361 millions d’habitants. La
population de l’Asie est de 833 millions d’habitants. En 2017, il y a
512 millions d’habitants en Europe et 4 milliards 457 millions en Asie.
12. Pour chaque 100 $ gagnés par un homme, une femme gagne 60 $ et un enfant 33,75 $. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4110
26 janvier 2018
Triangles magiques d’ordre 4
Comment peut-on distribuer les nombres de 1 à 9 dans la figure ci-après
formée de neuf cellules disposées en un triangle pour que la somme soit
la même sur chaque côté du triangle ? C’est ce que nous allons résoudre.
Dans un carré magique, il y a une seule somme possible par rangée. Dans
cette figure, il y a peut-être plus d’une somme. Allons voir.
La somme des nombres de 1 à 9 est 45. Si on divise 45 par 3, on obtient
15. Ce nombre 15 est-il une somme possible ? La réponse est non, car les
nombres des trois cellules des sommets appartiennent à deux rangées.
Posons que les nombres des trois cellules des sommets sont 1, 2 et 3. On
doit multiplier par 2 leur somme : ce qui fait 12. La somme des autres
nombres est 39. La somme totale est 51. Si on divise 51 par 3, on
obtient 17. La plus petite somme latérale sera 17 lorsque les nombres
des trois cellules des sommets sont 1, 2 et 3.
La somme des sommets dans chaque rangée est 3, 4 et 5. Pour compléter
chaque côté, on doit trouver des couples de nombres dont la somme est
respectivement 14, 13 et 12. Ces couples existent. Il y a donc au moins
une configuration. En voici une :
La somme suivante par rangée est 18. La somme indexée, soit celle qui
tient compte des cellules doubles, est 54. Comme la somme des entiers de
1 à 9 est 45. La somme des nombres des sommets devra être 9. Les
combinaisons possibles sont (1, 2, 6), (1, 3, 5) ou (2, 3, 4). Prenons
(1, 2, 6). La somme des sommets dans chaque rangée est 3, 7 et 8. Pour
compléter chaque rangée, on doit trouver des couples de nombres dont la
somme est respectivement 15, 11 et 10. Le 9 ne peut pas être placé. La
même situation se produit avec les deux autres combinaisons. Même si la
somme par rangée, soit 18, s’avérait possible, elle n’engendre pas de
solution.
Lorsque la somme latérale est 19, il existe au moins une configuration.
En voici une :
Lorsque la somme latérale est 20, il existe au moins une configuration.
En voici une :
On suppose que les sommets reçoivent 7, 8 et 9. La somme des trois
nombres est 24. La somme indexée est alors : 45 + 24 = 69. Or, 69 ÷ 3 =
23. La plus grande somme possible latérale est 23. Sauriez-vous trouver
au moins une configuration pour les sommes latérales 21, 22 et 23 ?
La somme latérale est 21. On n’a qu’à soustraire de 10 chacun des
nombres dont la somme latérale est 19. Voici cette configuration :
La somme latérale est 22. Il n’existe pas de configuration.
La somme latérale est 23. On n’a qu’à soustraire de 10 chacun des
nombres dont la somme latérale est 17. Voici cette configuration :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4075
12 janvier 2018
Carrés magiques d’ordre 5
Dans son livre
100 jeux numériques publié en
1973, au jeu 30, Pierre Berloquin demande de compléter un carré magique
d’ordre 5 avec les nombres de 6 à 25. La somme doit alors être 65 dans
chaque ligne, chaque colonne et chacune des deux diagonales.
Un lecteur de Récréomath m’a écrit
pour me demander si je connaissais une façon de résoudre le problème.
J’aurais aimé lui répondre positivement, mais peine perdue.
En réalité, le problème est très
difficile puisque les cinq nombres donnés ne semblent pas suivre une
règle de disposition. De plus, en 1973, l’Américain Richard Schroepel a
déterminé qu’il existe 275 305 224 carrés magiques d’ordre 5 avec les
nombres de 1 à 25.
Comme me l’a souligné mon
interlocuteur à la suite de mon message, il faudrait se tourner vers la
programmation. Voici la réponse de Berloquin dans son livre :
Par ailleurs, ce problème n’est
pas à réponse unique. Mon interlocuteur a noté que, dans la troisième
colonne, on : 11 + 15 = 26 et que, dans la cinquième colonne, on a 9 +
17 = 26. Comme aucun de ces nombres n’appartient à une diagonale, on
peut les permuter ligne par ligne. On obtient une deuxième
configuration :
À la suite de cette réponse, j’ai
remarqué que, dans chaque colonne, la somme des nombres de la deuxième
et de la quatrième ligne est égale est 26 : ce qui aurait pu être un
indice supplémentaire pour résoudre le problème.
En plus, comme 21 + 5 = 26 et que
les nombres ne sont pas dans une diagonale, on pourrait trouver d’autres
configurations avec cette nouvelle donnée. En voici une :
Des lecteurs pourraient-ils trouver d’autres configurations au problème de Berloquin ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4035
6 décembre 2017
Un problème de sous
Problème. Anne place 6 sous en un rectangle 2 × 3. Puis, elle entoure le
rectangle d’une première couronne. Celle-ci nécessite 14 pièces.
Combien de pièces seront nécessaires pour former une cinquième
couronne ?
Solution 1
La démarche qui nous vient d’abord à l’esprit est de former les
couronnes en dessinant les sous. Cela risque d’être long et fastidieux,
sans compter les risques d’erreurs.
Solution 2
On peut prendre des sous ou des
jetons. Le risque d’erreurs est fortement diminué.
Solution 3
On peut faire un tableau où R est le rang de la couronne, H1, la rangée
horizontale supérieure, H2, la rangée horizontale inférieure, C1 la
première colonne et C2 la dernière colonne. Pour chaque rangée, on donne
le nombre de sous nécessaires.
On remarque que d’une couronne à l’autre, le nombre de sous augmente de
2 dans chaque rangée : ce qui fait une augmentation de 8. La cinquième
couronne nécessite 46 sous.
Solution 4
Le rectangle initial est de 2 × 3. Il nécessite 6 sous.
La première couronne est dans un rectangle 4 × 5. Le rectangle contient
20 sous. On soustrait 6 et on obtient 14.
La deuxième couronne est dans un rectangle 6 × 7. Le rectangle contient
42 sous. On soustrait 20 et on obtient 22.
La troisième couronne est dans un rectangle 8 × 9. Le rectangle contient
72 sous. On soustrait 42 et on obtient 30.
La quatrième couronne est dans un rectangle 10 × 11. Le rectangle
contient 110 sous. On soustrait 72 et on obtient 38.
La cinquième couronne est dans un rectangle 12 × 13. Le rectangle
contient 156 sous. On soustrait 110 et on obtient 46. La cinquième
couronne nécessite 46 sous.
Problème complémentaire
Combien de pièces seront nécessaires pour former une 100e
couronne ?
Solution. D’une couronne à l’autre, le nombre de sous augmente de 8. On
peut trouver et appliquer une formule. Le nombre de sous d’une couronne
est égal à 8x + 6 où
x est le rang de la couronne.
Si x = 100, le nombre de sous
est de 806.
Conclusion
Si on avait connu cette formule, on aurait pu l’appliquer dans le
problème initial pour x = 5.
Ce qui donne bien 46 sous. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 4005
24 novembre 2017
Carré magique d’ordre 4 Par Jean-Marc Gervais
Le carré magique d’ordre 4 possède
notamment 5 propriétés intéressantes. Voici un carré général :
On appelle S la somme commune aux
lignes, aux colonnes et aux diagonales. Cette somme est égale à 34 dans
le cas où on prend tous les nombres entiers de 1 à 16.
1) La somme des nombres situés
dans les coins est égale à S.
A
+ D + P + M = S
2) La somme des 4 nombres centraux
est égale à S.
F + G + J + K = S
3) La somme des nombres latéraux
et situés sur des côtés parallèles est égale à S. (Un nombre latéral est
un nombre situé sur un côté du carré, mais pas dans un coin).
B
+ C + N + O = S
E
+ I + H + L = S
De ces propriétés, on en déduit
deux autres :
4) La somme de 2 nombres situés
dans des coins opposés est égale à la somme des 2 nombres centraux et
situés sur la diagonale perpendiculaire.
A + P = J + G ; D + M = F + K
5) La somme de 2 nombres latéraux
et situés sur le même côté est égale à la somme des 2 nombres situés
dans les coins et sur le côté parallèle.
E + I = D + P ; H + L = A + M ; B + C = M + P ; N + O = A + D
Exemple 1.
Ce carré est magique de somme 34.
De plus, la somme des nombres situés dans chaque carré 2 × 2 des coins
est égale à 34. Ceci n'est pas toujours vrai.
Exemple 2.
Dans le carré magique ci-dessus,
la somme des nombres situés dans chaque carré 2 × 2 des coins n'est pas
égale à 34. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3980
14 novembre 2017
Somme de deux carrés
On peut additionner mentalement
deux carrés assez facilement, mais à certaines conditions. On peut le
faire seul ou requérir la coopération d’une autre personne. Voici
comment on peut procéder :
1. Vous demandez de vous donner un
nombre qui ne contient pas de zéro entre 10 et 59.
2. Vous soustrayez 1 au dernier
chiffre. Ce chiffre devient la dizaine de l’autre nombre.
3. Vous trouvez le complément du
chiffre de la dizaine, c’est-à-dire 10 – le chiffre de la dizaine du
nombre donné. Ce chiffre devient le dernier de l’autre nombre.
4. Vous énoncez ce dernier nombre.
5. Vous dites que vous allez faire
instantanément la somme des carrés du nombre de départ et du dernier
nombre.
6. Pour trouver la somme
mentalement, on élève au carré chacun des chiffres du nombre donné et on
fait la somme. On retient une autre fois la somme. Par exemple, si la
somme est 34, le résultat final sera 3434.
Voici un exemple : Quelqu’un dit
25. En réponse, vous dites 48. En effet, 5 – 1 = 4 et 10 – 2 = 8. Vous
faites : 22 + 52 = 29. La somme est 2929. On peut
vérifier que 252 + 482 = 2929.
Si, à l’étape 6, on trouve un
nombre d’un seul chiffre, on fait comme si on avait un 0 en avant. Par
exemple, quelqu’un choisit 12. Votre riposte sera 19. Or, 12 +
22 = 5. La somme est 0505 ou 505. En effet, 122 +
192 = 505. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3945
31 octobre 2017
Petites démonstrations
Il est
rarement facile de faire une démonstration en mathématiques. Il faut
connaître les propriétés des objets mathématiques concernés et être
capable de les appliquer à bon escient. Voici trois exemples de
problèmes de démonstration :
1. Un carré magique
Démontrez
qu’il est impossible, lorsque le 1 est dans la position indiquée, de
construire un carré magique d’ordre 3 avec les nombres de 1 à 9. La
somme de chaque ligne, chaque colonne et chaque diagonale doit être
égale à 15.
Démonstration. De par sa position dans le carré, le 1 appartient à trois
rangées : une ligne, une diagonale et une colonne. Or, avec 1, il
n’existe que deux combinaisons dont la somme est 15 : (1, 8, 6) et (1,
5, 9). D’où, il est impossible de construire un carré magique d’ordre 3
selon ces conditions.
2. Un cryptarithme
Dans ce genre
de problème, il s’agit d’attribuer un chiffre différent à chaque lettre.
Par exemple, si j’écris MA + MA = SA, une réponse est M = 1, A = 0 et S
= 2.
Démontrez
qu’il est impossible d’obtenir une réponse pour le cryptarithme
suivant :
MARC + LISE =
RUTH
Démonstration. Le cryptarithme contient 11 lettres différentes. Or, il
n’y a que 10 chiffres. D’où, il est impossible d’obtenir une réponse.
3. Le jour de la semaine
Andrée a
obtenu son permis de conduire le lundi 15 juillet 2013. Son frère l’a
obtenu 300 jours plus tard.
Démontrez
que, pour le frère, ce n’était pas un lundi.
Démonstration. On pourrait être tenté de trouver le jour de la semaine.
En faisant cela, on aurait montré et non démontré que ce n’était pas un
lundi. Pour démontrer, on fait 300 ÷ 7 = 42, reste 6. Traduit dans la
réalité, ce résultat indique qu’il y a un écart de 42 semaines et 6
jours entre les deux événements. Pour que ce soit le même jour de la
semaine, il faudrait que le reste soit 0. D’où, ce n’était pas un lundi
quand le frère a obtenu son permis. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3915
19 octobre 2017
Livre : 1001 nombres charmants
Dans mon site Récréomath, j’ai édité un
livre : 1001 nombres charmants. Ce recueil de 572 pages sur papier
présente les principales propriétés des entiers de 0 à 1000. Pour chaque
nombre, il est possible de trouver un très grand nombre de propriétés.
J’ai essayé d’indiquer celles qui n’apparaissent pas à première vue.
Voir :
http://www.recreomath.qc.ca/ed_nombres_charm_a.htm
Voici un extrait du texte de présentation :
« Chaque nombre a son entité propre. Les uns
prennent plus de place que d’autres. On dit qu’ils sont plus
extravertis. Tous ont des propriétés spécifiques. Il y a, par exemple,
les nombres premiers qui se caractérisent par le fait qu’ils ont
seulement deux diviseurs : 1 et lui-même. Dans la séquence des entiers,
ils arrivent de façon inopinée.
Il y a les nombres pairs, ces choyés qui sont
divisibles par 2. Il y en a une infinité. On les reconnaît par leur
dernier chiffre : 0, 2, 4, 6 et 8. À l’exception de 0, tout nombre qui
n’est pas pair est impair. Il y en a aussi une infinité. Ceux-ci se
définissent par la négative et sont coincés entre deux pairs.
Il y a les carrés, les cubes, les
triangulaires. Tous sont en nombre infini. Cela fait beaucoup de classes
de nombres infinis. Il est très difficile d’appréhender l’infini avec
rigueur. Ce sujet a été un important sujet de discorde dans l’histoire
des mathématiques.
Nous avons accordé une large place aux nombres
triangulaires, ceux qui sont formés par une suite d’entiers
consécutifs à partir de 1. Par exemple, 21 est triangulaire, car il est
la somme de 1, 2, 3, 4, 5 et 6. »
Voici les principales propriétés de 52, telles
que présentées dans le recueil :
Décagonal de rang 4 : 10 + 12 + 14 + 16 = 52.
Somme des quatre triangulaires consécutifs : 3D + 4D
+ 5D
+ 6D
= 52.
52
= 13(1 + 3)
52
= 2D
+ 72
52
= 42 + 62
52
= 52 + 33
52
= 23 + 24 + 7D
522
=
202 + 482
Arrangements des mêmes chiffres de part et d’autre
52
= 25 + 52 - 5
523
= 140 608 = (1 - 40 + 60 - 8)3
Valeur de SIX lorsque l’on additionne les rangs de ses lettres.
Nombre de pièces dans un jeu de cartes.
Nombre de façons de disposer cinq pièces du jeu d’échecs sur une étagère
de cinq tablettes. »
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3885
7 octobre 2017
Les combinaisons
En termes d’habillement, une
combinaison est un vêtement de travail ou de sport qui combine veste et
pantalon en une pièce. En québécois, une combinaison est un
sous-vêtement masculin d’une seule pièce des épaules aux pieds. En
mathématiques, une combinaison est un sous-ensemble composé d’un nombre
d’objets choisis parmi un nombre déterminé d’objets sans égard à l'ordre
dans lequel on les dispose.
Problème. Trouvez toutes les
façons de combiner trois lettres à partir d’un ensemble de huit lettres.
Solution. Il
faut procéder de façon systématique pour ne pas en oublier. Soit A, B,
C, D, E, F, G et H les huit lettres. On commence par trouver toutes les
combinaisons ayant un A toujours en suivant l’ordre alphabétique :
ABC ABD
ABE ABF
ABG ABH
ACD ACE
ACF ACG
ACH
ADE ADF
ADG ADH
AEF AEG
AEH
AFG AFH
AGH
Cela donne 21 combinaisons.
On commence maintenant par B. On
a :
BCD
BCE BCF
BCG BCH
BDE
BDF BDG
BDH
BEF BEG
BEH
BFG BFH
BGH
Cela donne 15 combinaisons.
En commençant par C, on obtient 10
combinaisons. En commençant par D, on obtient 6 combinaisons. En
commençant par E, on obtient 3 combinaisons. En commençant par F, on
obtient 1 combinaison. Je laisse au lecteur le soin de les trouver. En
tout, on aura 56 combinaisons.
Il existe une
formule pour trouver le nombre de combinaisons dans un ensemble sans
être obligé de toutes les énumérer.
Prenons le
problème précédent. Soit n le
nombre total de lettres, soit p
le nombre de lettres par combinaison, le nombre de combinaisons est :
Le point d’exclamation est mis
pour factorielle. Par exemple, 8!, qui se lit 8 factorielle, est 1 × 2 ×
3 × 4 × 5 × 6 × 7 × 8.
Dans ce cas,
on a :
On n’a pas
besoin de faire toutes les multiplications. On se contente de
simplifier. Le résultat est bien 56. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3855
25 septembre 2017
Triple X magique
Comment peut-on distribuer les nombres de 1 à 11 dans la figure ci-après
formée de 11 cellules disposées en X pour que la somme soit la même dans
chaque rangée de trois cercles ? C’est ce que nous allons résoudre.
Il faut d’abord déterminer la somme possible pour les rangées de la
figure. Pour ce faire, on attribue à chaque cellule un indice qui
correspond au nombre de rangées qui passent par cette cellule.
Les sept cellules marquées 2 sont à l’intersection de deux rangées. Les
quatre cellules marquées 1 appartiennent à une seule rangée. La somme
des entiers de 1 à 11 est 66. Si chaque cellule était marquée 2, la
somme totale serait 132.
On suppose que les entiers de 1 à 7 sont placés dans les cellules
marquées 2. On peut écrire : (1 + 2 + 3 + 4 + 5 + 6 + 7) × 2 + (8 + 9 +
10 + 11) × 1 = 56 + 38 = 94. Il y a six rangées. On fait : 94 ÷ 6 = 15
⅔. La plus petite somme par rangée est probablement 16. On dit
probablement parce qu’on
n’est pas certain qu’il y aura possibilité de répartir les nombres de 1
à 11 avec cette somme.
On suppose que les entiers de 1 à 4 sont placés dans les cellules
marquées 1. On peut écrire : (1 + 2 + 3 + 4) × 1 + (5 + 6 + 7 + 8 + 9 +
10 + 11) × 2 = 10 + 112 = 122. Il y a six rangées. On fait : 122 ÷ 6 =
20 ⅓. La plus grande somme par rangée est probablement 20.
Somme par rangée : 16 La somme totale doit être 16 × 6 = 96. La somme des quatre éléments des coins est donc 132 – 96 = 36. Les combinaisons de 36 sont : (6, 9, 10, 11) et (7, 8, 10, 11). Voici une configuration :
Somme par rangée : 17
La somme totale doit être 17 × 6 = 102. La somme des quatre éléments des
coins est donc 132 – 102 = 30. Les combinaisons de 30 sont : (1, 8, 10,
11), (2, 7, 10, 11), (3, 6, 10, 11), (4, 5, 10, 11), (2, 8, 9, 11), (3,
7, 9, 11), (4, 6, 9, 11). Voici une configuration :
Somme par rangée : 18
La somme totale doit être 18 × 6 = 108. La somme des quatre éléments des
coins est donc 132 – 108 = 24. Je laisse au lecteur le soin de trouver
toutes les combinaisons de quatre nombres différents parmi les entiers
de 1 à 11. Voici une configuration où la combinaison est (1, 2, 10, 11)
:
Somme par rangée : 19
On choisit une configuration dont la somme par rangée est 17. De 12, on
soustrait chaque élément. C’est une configuration dite complémentaire.
Voici une configuration qui est complémentaire à celle donnée
précédemment lorsque la somme est 17 :
Somme par rangée : 20
Voici une configuration qui est complémentaire à celle dont la somme par
rangée est 16 :
Conclusion. Il existe au moins une configuration pour chaque somme par
rangée de 16 à 20. Ce sont les cinq sommes possibles. Par ailleurs,
chaque somme a un nombre fini de configurations. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3830
13 septembre 2017
Dénombrement de figures
Dans la figure ci-après, chaque L est constitué de quatre petits carrés.
On demande de déterminer le nombre de L dans cette figure.
Tentez de résoudre le problème. Après avoir réussi ou pas, lisez les
cinq stratégies que je vous propose.
Stratégie 1. On compte les L en les pointant un à un. Toutefois, avec
les yeux seulement, il est difficile de les compter.
Stratégie 2. On imprime la figure. On compte les L en les colorant en
foncé ou en faisant une marque.
Stratégie 3. On considère les deux rangées horizontales du bas. On peut
y compter l’équivalent de 5,5 L. Comme la figure est composée de 8
rangées horizontales, on multiplie 5,5 par 8 et on divise par 2.
Stratégie 4. On considère les deux rangées verticales de droite. On peut
y compter l’équivalent de 4 L, soit une moyenne de 2 L par rangée
verticale. Comme la figure est composée de 11 rangées verticales, on
multiplie 2 par 11.
Stratégie 5. La figure est un rectangle 8 × 11. On peut y compter 88
petits carrés. Comme chaque L occupe 4 petits carrés, on divise 88 par
4.
On aura compris qu’il y a 22 L dans cette figure.
Conclusion. Souvent à partir d’un problème simple, il est possible
d’appliquer plusieurs stratégies. Après avoir trouvé une réponse, il est
recommandé d’utiliser une seconde stratégie qui sert alors de
vérification. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3805
3 septembre 2017
Un nouveau livre d’énigmes Les éditions Goélette viennent de publier un autre de mes livres d’énigmes. Il est intitulé 675 énigmes. C’est un livre de 384 pages qui contient, comme son titre l’indique, 675 énigmes de différents genres. Pas besoin d’avoir de grands talents pour résoudre ces énigmes. Un peu de logique et des connaissances élémentaires suffisent.
Voici, à titre d’exemple, la première énigme du livre :
1. Proche du diable
Je n’appartiens pas à une échelle.
J’appartiens plutôt à un barreau.
Je défends parfois le diable.
Je suis aussi un fruit.
Qui suis-je ?
(Un
avocat)
Pour ceux et celles qui veulent titiller et conserver actives leurs
neurones. Le prix suggéré de l’éditeur est 12,95 $. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3745
17 juin 2017
Des
petits exercices
Un père m’a posé la question
suivante : « Que proposez-vous comme exercices pour un enfant de 8 ans
en 2e année ? »
Réponse : Je
ne connais pas le niveau de capacité en mathématiques chez votre enfant
de deuxième année. Je vous fais des suggestions que vous pourrez adapter
à son état de connaissances. Il faudrait insister sur le calcul mental
en présentant des situations ludiques. L’apprentissage de la table
d’addition et celle de multiplication devrait être la priorité.
Situation 1.
Avec votre enfant, découpez des jetons que vous numérotez de 1 à 10. Il
serait préférable de constituer deux de ces ensembles. Marquez des
jetons avec les signes +, – et = selon vos besoins.
Demandez à
votre enfant de placer un jeton numéroté sur la table. Ajoutez un signe
+ ou –. Demandez à votre enfant de placer un autre jeton numéroté. Posez
le signe =. Demandez à votre enfant de trouver le résultat ou encore
d’écrire la réponse sur un jeton non numéroté.
Situation 2. Adaptez la situation
1 avec la multiplication et la division.
Situation 3. Inventez des petites
histoires où l’enfant devra résoudre le problème. Exemple 1. Grand-papa
a 5 carottes. Pendant la nuit, un lapin s’empare de 2 carottes. Combien
reste-t-il de carottes à grand-papa ?
Exemple 2. Le Petit Chaperon Rouge
apporte 4 pommes à sa grand-maman. En chemin, une dame lui donne 3
pommes. Combien de pommes le Petit Chaperon Rouge pourra-t-il donner à
sa grand-maman ?
Mettez à profit le vécu de
l’enfant et le vôtre pour rendre les histoires crédibles aux yeux de
l’enfant.
Bonne chance ! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3715
2 juin 2017
Divisibilité en magie
Il est bon de
présenter de temps à autre aux élèves des trucs qui relèvent de la
magie. Voici une activité :
Matériel :
tableau, craie ou marqueur, calculatrice chez les élèves
Préparation.
On tire quatre traits sur le tableau. L’enseignant pourra écrire les
chiffres sur ces traits.
L’enseignant
dit :
« Avec vous,
je vais composer des nombres de quatre chiffres qui sont divisibles par
4, c’est-à-dire qu’il n’y pas de reste lorsqu’on fait la division.
Vous allez me
donner un chiffre. [L’enseignant place le chiffre en première position,
soit complètement à gauche.]
À mon tour,
je vais écrire un chiffre. [L’enseignant le place en deuxième position.]
Donnez-moi un
autre chiffre. [L’enseignant le place en troisième position.]
À mon tour,
je vais placer un chiffre en quatrième position. [Si le dernier chiffre
donné est pair, l’enseignant écrit 0, 4 ou 8. Si le dernier chiffre
donné est impair, il écrit 2 ou 6.]
Vérifiez avec
votre calculatrice en divisant ce nombre par 4. »
Exemple. Un
élève choisit 5. L’enseignant le place en première position.
L’enseignant choisit 9 et le place en deuxième position. Un élève
choisit 7 qui est placé en troisième position. L’enseignant choisit 6 et
le place en quatrième position. Le nombre est 5976. Il est divisible par
4.
On doit
suivre les règles suivantes :
• Dans les
trois premières positions, on peut placer n’importe lequel chiffre, sauf
0 au début.
• En
quatrième position, on doit placer un chiffre pair selon la règle
énoncée précédemment.
À la fin,
vous dites aux élèves : « Essayez de trouver le truc. Je vous
l’expliquerai la semaine prochaine. Un élève prendra alors ma place pour
faire la même activité. »
Comme
supplément, l’enseignant pourrait choisir d’écrire les chiffres dans
n’importe quel ordre à la condition d’adapter les règles pour les deux
derniers chiffres. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3670
14 mai 2017
La Fête des Mères
La Fête des Mères qui vise à souligner le dévouement et
l’implication des mères de famille est soulignée dans la plupart des
pays. Au Québec, elle a lieu le deuxième dimanche de mai. Elle arrive au
plus tôt le 8 mai et au plus tard le 14 mai.
Voici trois situations mathématiques inspirées par cette fête :
Situation 1. Connaissant le quantième de la
Fête des Mères en une année, comment trouver le quantième de l’année
suivante ?
Étapes
• Quand l’année cherchée est ordinaire, on soustrait 1 au quantième
donné.
• Quand l’année cherchée est bissextile, on soustrait 2 au
quantième donné.
• Si le résultat est plus petit que 8, on additionne 7.
• Si le résultat est plus grand ou égal à 8, c’est le quantième
cherché
En 2017, cette fête a lieu le 14 mai. Quel sera le quantième en
2018 ? On fait : 14 – 1 = 13. Ce sera le 13 mai en 2018.
En 1999, cette fête a eu lieu le 9 mai. Quel a été le quantième en
2000 ? On fait : 9 – 2 = 7 et 7 + 7 = 14. En 2000, la fête a eu lieu le
14 mai.
Situation 2. Connaissant le jour de la semaine
du 1er janvier d’une année, comment trouver le quantième de
la Fête des Mères en cette même année ?
Étapes
• Quand l’année est ordinaire, le 1er mai sera le jour
de la semaine suivant celui du 1er janvier.
• Quand l’année est bissextile, le 1er mai sera le
deuxième jour de la semaine suivant celui du 1er janvier.
• On identifie le quantième du premier dimanche après le 1er
mai, puis du second dimanche.
En 2018, le 1er janvier sera un lundi. Le 1er
mai sera un mardi. Le premier dimanche sera le 6 et le second le 13. En
2018, la fête sera célébrée le 13 mai.
En 2020, le 1er janvier sera un mercredi. Le 1er
mai sera un vendredi. Le premier dimanche sera le 3 et le second le 10.
En 2020, la fête sera célébrée le 10 mai.
Situation 3. Pour une année donnée du 21e siècle,
comment trouver le quantième de la Fête des Mères ?
Étapes
•
On prend les deux derniers chiffres de
l’année.
•
On divise ce nombre par 4 et on retient le
quotient en ignorant le reste.
•
On additionne les deux derniers chiffres de
l’année et le quotient.
•
On divise la somme par 7 et on conserve
seulement le reste.
• On
soustrait le reste de 14.
Quel sera le quantième en 2025 ?
On 25 ÷ 4 = 6 reste 1. On retient 6. On fait : 25 + 6 = 31. On fait : 31
÷ 7 = 4 reste 3 et 14 – 3 = 11. En 2025, la fête aura lieu le 11 mai,
tout comme, par exemple, en 2014, 2031, 2042 et 2053. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3630
26 avril 2017 Un solitaire géométrique
Vous pouvez construire un solitaire ou, si vous voulez, un casse-tête
géométrique. Confectionnez quatre cubes de même volume. Placez-les en
une colonne. Vous obtenez ainsi un prisme droit à base carrée. Coloriez
chaque face de côté du prisme d’une seule couleur. Vous avez besoin de
quatre couleurs.
Voici un exemple où on donne les patrons des quatre cubes :
Pour s’aider à assembler les cubes, on commence par compter la fréquence
des couleurs sur chaque facette. Il y a cinq facettes vertes, six
jaunes, six rouges, sept bleues. Seize facettes doivent apparaître sur
les côtés du prisme. Les facettes cachées seront une verte, deux jaunes,
deux rouges et trois bleues. On place les cubes en considérant ces
données. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3570
2 avril 2017 Petits problèmes plaisants
Je publie
dans ce blogue un nouveau livre de ma composition intitulé
Petits problèmes plaisants. Il contient 150 problèmes courts qui
font appel à des connaissances mathématiques et logiques élémentaires.
Les problèmes s’adressent aux amateurs de 9 à 99 ans. Les stratégies de
résolution qui s’appliquent sont généralement à la portée des débutants. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3545
23 mars 2017
Un
nouveau livre
Je publie dans ce blogue un recueil de ma composition intitulé
Jeux de grilles. Il contient 150 problèmes comportant au moins une
grille. Les problèmes font appel à des connaissances élémentaires
d’arithmétique et de logique. On doit composer des carrés magiques, des
carrés latins et des nombres croisés, calculer le nombre de carrés ou de
rectangles dans une grille, transformer des lettres en chiffres,
déplacer des jetons ou encore biffer des nombres qui ont une même
propriété. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3505
7 mars 2017
Trucs de calcul mental
On ne le dira
jamais assez. Le calcul mental est d’une importance capitale. Il n’est
pas nécessairement rapide. Tout comme on montre à l’enfant à attacher
ses chaussures, on doit appuyer sur le calcul mental. Voici trois
exemples où l’enfant peut pratiquer le calcul mental sous un aspect
récréatif :
Premier exercice
On présente à
un jeune enfant une grille de nombres. Il doit repérer les groupes de
deux nombres dont la somme est donnée. En cours de route, il colorie les
cases ou biffe les deux nombres appropriés. Dans cette grille, la somme
est 15.
À la fin, il additionne les nombres qui restent.
Solution. Les nombres qui restent sont 6 et 7. Leur somme est 13.
Les parents peuvent composer des grilles adaptées aux connaissances
de l’enfant.
Deuxième exercice
L’enfant doit compléter la grille pour que la somme soit 17 sur
chaque ligne et dans chaque colonne.
Solution. La grille remplie est :
Troisième exercice
Dans la grille, l’enfant doit trouver combien de couples de nombres
voisins horizontalement et verticalement ont une somme de 15.
Solution. On trouve sept couples. Horizontalement, on a : (7, 8),
(4, 11), (5, 10), (6, 9). Verticalement, on a : (3, 12), (9, 6), (1,
14).
Par surcroit, ce dernier exercice apprend à l’enfant à procéder de
façon systématique.
L’introduction d’un aspect ludique dans ces exercices peut procurer à
l’enfant un certain intérêt, beaucoup plus que s’il devait faire une
série d’additions sur une feuille. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3450
13 février 2017
Cubes magiques
Il existe plusieurs formes de cubes magiques. L’une d’elles a rapport
aux faces. En plaçant 12 nombres sur les arêtes pour que la somme soit
26 sur chaque face, on obtient un cube magique sur les faces. Par
exemple, dans la figure ci-dessous, on a : 12 + 11 + 1 + 2 = 26, 12 + 3
+ 6 + 5 = 26, etc.
Nous donnons une technique simple pour trouver des solutions lorsqu’on
considère quatre faces sur six. Dans la grille ci-après, les losanges
AKBJ, BGCH, LDMC et AEDF sont les quatre faces. Voici comment on
procède :
• On transforme le cube en une grille carrée où les 12 lettres
correspondent aux entiers de 1 à 12. Chaque losange correspond à une
face.
• On fait les combinaisons de deux nombres dont la somme est 13.
1 2
3
4 5
6
12 11
10 9
8 7
• On place en A et B deux nombres dont la somme est 13.
• On place en D et C deux nombres dont la somme est 13.
• On fait (A + D). On écrit les combinaisons possibles de deux nombres
pour cette somme.
• On fait (B + C). On écrit les combinaisons possibles de deux nombres
pour cette somme.
• Dans les combinaisons possibles, on cherche quatre nombres dont la
somme est 26 et qui appartiennent à deux combinaisons de 13. On les
place de façon appropriée en E, F, G et H. Si les quatre nombres
n’existent pas, on revient au début et on fait d’autres essais.
• Si les quatre nombres existent, il reste deux combinaisons. On les
place en J, K, L et M.
Voici une première grille où la somme des nombres est 27 autour de la
case centrale :
Voici une deuxième grille où la somme des nombres est 29 autour de la
case centrale :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Suite des propos mathématiques | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

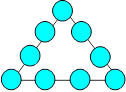


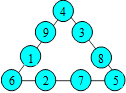
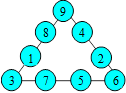
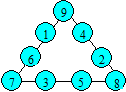

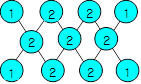
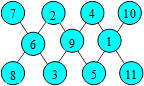
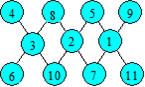

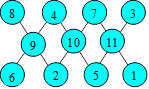
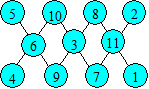
 Sur
le dos de la couverture, l’éditeur a écrit : « Faites appel à votre
esprit de déduction pour percer ces 675 énigmes ! Mais gare aux pièges
et aux fausses pistes !
Sur
le dos de la couverture, l’éditeur a écrit : « Faites appel à votre
esprit de déduction pour percer ces 675 énigmes ! Mais gare aux pièges
et aux fausses pistes !